Minule som písal čo sú to vlastne derivácie, Spomenul som v tejto súvislosti aj integrály ako opak derivácie. Integrovaním derivovanej funkcie dostaneme pôvodnú funkciu. Výpočet je opačný, pre výpočet mocninovej derivácie počítame podľa vzorca. ![]() V zásade platí, že keď poznáme deriváciu vieme nájsť integrál podľa daných vzorcov inegrálov. Integrál sa označuje pretiahnutým eskom, d je diferenciál, ten nám udáva ktorú hodnotu budeme integrovať. Niekedy má nezanedbateľný význam, napíšem niečo o tom v inom blogu z fyziky. Ako príklad uvediem integrovanie rýchlosti na čase podľa minulého blogu. Keď integrujeme rýchlosť podľa času dostaneme dráhu s. V predchádzajúcom blogu dráha bola závislá na druhej mocnine času s=t2. Derivovaním tejto funkcie podľa času bola okamžitá rýchlosť. Podľa tejto derivácie je okamžitá rýchlosť číselne vyjadrená dvojnásobkom v danom čase v=2t. Keď rýchlosť bodu na dráhe stúpa s druhou mocninou času, tak zrýchlenie je vtedy rovnomerné. Integrovaním času a dostaneme dráhu ktorú prejde bod na dráhe za daný čas.
V zásade platí, že keď poznáme deriváciu vieme nájsť integrál podľa daných vzorcov inegrálov. Integrál sa označuje pretiahnutým eskom, d je diferenciál, ten nám udáva ktorú hodnotu budeme integrovať. Niekedy má nezanedbateľný význam, napíšem niečo o tom v inom blogu z fyziky. Ako príklad uvediem integrovanie rýchlosti na čase podľa minulého blogu. Keď integrujeme rýchlosť podľa času dostaneme dráhu s. V predchádzajúcom blogu dráha bola závislá na druhej mocnine času s=t2. Derivovaním tejto funkcie podľa času bola okamžitá rýchlosť. Podľa tejto derivácie je okamžitá rýchlosť číselne vyjadrená dvojnásobkom v danom čase v=2t. Keď rýchlosť bodu na dráhe stúpa s druhou mocninou času, tak zrýchlenie je vtedy rovnomerné. Integrovaním času a dostaneme dráhu ktorú prejde bod na dráhe za daný čas.
![]() Dostali sme pôvodnú funkciu dráhy na čase s=t2.
Dostali sme pôvodnú funkciu dráhy na čase s=t2.
Takou praktickou ukážkou je výpočet objemu pravidelného ihlana. Ihlan ktorý má výšku rovnakú ako všetky štyri strany a jeho výška ide stredom kocky je rovnomerný ihlan. objem kocky je Vk=a3 . Môžeme objem vypočítať aj ako násobok podstavy kocky Spk=a2 výškou a. Integráciu si môžeme predstaviť tak, že sčítavame jednotlivé elementárne diely. Keby sme integrovali podstavu kocky, znamená to, že sčítavame elementárne podstavy nad sebou do výšky a. Tak dostaneme objem ihlanu Vi=a3/3. Vzorec podľa integrálu
![]() Tak sme prišli na to, že objem všetkých špicatých telies je 1/3 objemu ich pravidelných telies, válec, hranol aj pri gule je to niečo podobné, tiež sa to počíta integrálom ale je to trochu zložitejší integrál.
Tak sme prišli na to, že objem všetkých špicatých telies je 1/3 objemu ich pravidelných telies, válec, hranol aj pri gule je to niečo podobné, tiež sa to počíta integrálom ale je to trochu zložitejší integrál.
Viac sa používajú tzv. určité integrály
Vynikajúci príklad na použitie určitých integrálov je výpočet plochy rotačného telesa. Dole je symetrické teleso, ktoré má po povrchu je krivka. Otáča sa okolo osy x. Polomer je na osi y a je závislý od bodu na osi x. Vyznačená plocha na grafe je určitý integrál funkcie s. Funkcia s je vrchná čiara na ploche. Na grafe je nakreslena uržitá časť plochy rotačného telesa o dĺžke Δx. Na osi y môžeme odrátať približný polomer. Vynásobením polomeru 2π a dĺžkou Δx dostaneme približnú plochu pásika. Keby to bol rovný válec plocha by bola presná. Válčeky nemajú rovnaký polomer, keby som chcel približne výpočítať plochu celého rotačého telesa, musím nasekať čo najmenšie kúsky Δx, vynásobiť a spočítať násobky. Čím budú menšie rovnaké Δx, tak výsledok bude presnejší.
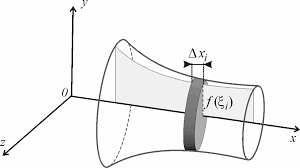 Keď vyberieme na osi x malý úsek Δx, tak na osy y dostaneme premietnutím zmenu Δy. Zmeny Δx a Δy vytvárajú pravouhlý trojuholník. Keď si označíme spojnicu zmien Δx a Δy zmenou Δs, môžeme si vyjadriť je veľkosť podľa pytagorovej vety
Keď vyberieme na osi x malý úsek Δx, tak na osy y dostaneme premietnutím zmenu Δy. Zmeny Δx a Δy vytvárajú pravouhlý trojuholník. Keď si označíme spojnicu zmien Δx a Δy zmenou Δs, môžeme si vyjadriť je veľkosť podľa pytagorovej vety![]()
Tento vzorec si môžeme upraviť tak, že vydelíme pravú stranu rovnice Δx a následne ju vynásobíme podľa rovnice 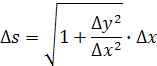 Keby sme celé teleso rozkúskovali na rovnaké malé časti Δx tak ich súčet nám dá približnú veľkosť celej dráhy s.
Keby sme celé teleso rozkúskovali na rovnaké malé časti Δx tak ich súčet nám dá približnú veľkosť celej dráhy s.
Keď budeme uvažovať zmeny elementárne tak dostaneme diferenciály a pomer diferenciálov je derivácia. S toho si môžeme odvodiť diferenciál ds podľa rovnice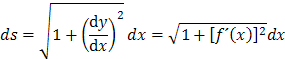
Odvodením z toho dostaneme integrál pre výpočet plochy rotačného telesa Sr. Funkciu rotačného telesa musíme poznať, alebo si ju môžeme odvodiť. Znaky a a b na integrále označujú body na osy x . Medzi nimi budeme počítať obsah plášťa. Bod a je bližšie k nule.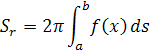 Z toho vzorec pre výpočet povrch rotačného telesasi môžeme odvodiť podľa určitého integrálu
Z toho vzorec pre výpočet povrch rotačného telesasi môžeme odvodiť podľa určitého integrálu
Najjednoduchší príklad je výpočet plášťa kužeľa. Rez kúžeľa vytvára medzi osami x y pravouhlý trojuholník. V nule je vrchol kúžeľa a na osi x je výška kúžeľa h. V bode h je pravý uhol a výška strany určuje polomer podstavy kužeľa r. Prepona je označená s, je to dĺžka plášťa od vrcholu po podstavu. výpočet je jednoduchý
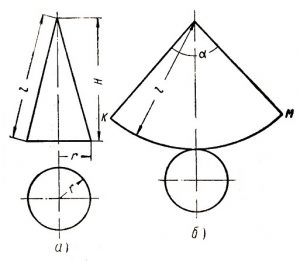 Vypočítame plochu kruhového výseku o polomere s a dĺžke oblúka 2πr. Strana s je určená podľa prvého obrázka, vypočítame ju pytagorovou vetou. vzorec je
Vypočítame plochu kruhového výseku o polomere s a dĺžke oblúka 2πr. Strana s je určená podľa prvého obrázka, vypočítame ju pytagorovou vetou. vzorec je![]() Keby sme to chceli riešiť integrálom potrebujeme vedieť akú funkciu bude mať strana s. Funkcia priamky sa určí podľa vzorca
Keby sme to chceli riešiť integrálom potrebujeme vedieť akú funkciu bude mať strana s. Funkcia priamky sa určí podľa vzorca ![]() My poznáme y, x, b=0 ale nepoznáme konštantu. Hodnoty sú x=h, y=r. Z toho vychádza vzorec pre konštantu
My poznáme y, x, b=0 ale nepoznáme konštantu. Hodnoty sú x=h, y=r. Z toho vychádza vzorec pre konštantu
![]() Priamka s zviera s osou určitý uhol φ. Tangens tohto uhla je derivácia tejto funcie. Keď si tieto hodnoty dosadíme do integrálu dostavame vzorec
Priamka s zviera s osou určitý uhol φ. Tangens tohto uhla je derivácia tejto funcie. Keď si tieto hodnoty dosadíme do integrálu dostavame vzorec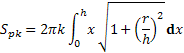 Konštantu neitegrujeme preto je pred integrálom. Dosadením do výpočtu dostaneme vzorec
Konštantu neitegrujeme preto je pred integrálom. Dosadením do výpočtu dostaneme vzorec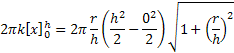 Po úprave dostanem výslednú hodnotu. Výsledok výpočtu plochy plášťa kužeľa je rovnaký ako v prvom vzorci.
Po úprave dostanem výslednú hodnotu. Výsledok výpočtu plochy plášťa kužeľa je rovnaký ako v prvom vzorci. 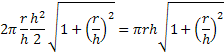
Keď nepoznáme vzorec pre objem gule, nemôžeme odvodiť vzorec pre povrch gule bez integrálov. Je to už zložitejšie odvodenie pre toho kto nepozná integrály, ale dá sa veľmi ľahko odvodiť povrch gule pomocou integrálov. obsahu povrchu gule. 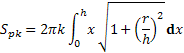 Funkcia je odvodená z rovnici kružnice.
Funkcia je odvodená z rovnici kružnice.
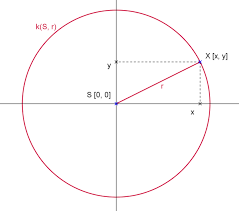
Odvodím rovnicu z obrázka hore. Na kružnici je bod X spája polomer r body x a y. Je to pravouhlý trojuholník a z neho môžeme odvodiť rovnicu,funkciu kružnice y ktorá má tvar ![]() Znamienko ± označuje či sa bude polkružnica nachádzať na kladnej alebo zápornej y. Počítať deriváciu budeme na kladnej ypsilonovej osi. Je to zložená derivácia, pretože derivujeme iba x. Počíta sa tak, že sa najprv zderivuje celá funkcia a potom iba x. Derivácie sa vynásobia podľa vzoru
Znamienko ± označuje či sa bude polkružnica nachádzať na kladnej alebo zápornej y. Počítať deriváciu budeme na kladnej ypsilonovej osi. Je to zložená derivácia, pretože derivujeme iba x. Počíta sa tak, že sa najprv zderivuje celá funkcia a potom iba x. Derivácie sa vynásobia podľa vzoru![]()
Ke´ď to upravíme a vložíme pod odmocninu dostávame vzorec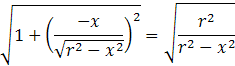 vložením do integrálu dostávame vzorec
vložením do integrálu dostávame vzorec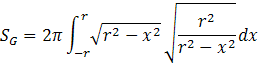 Roznásobením integrálu dostaneme konečný vzorec
Roznásobením integrálu dostaneme konečný vzorec ![]() Na xovej osi sú vzdialenosti 0+r a záporná 0-r s toho s toho dostaneme konečný vzorec
Na xovej osi sú vzdialenosti 0+r a záporná 0-r s toho s toho dostaneme konečný vzorec
Tak sme pomocou integrálov diferenciálov a derivácii prišli výpočet na povrchu gule.
![]() Vzorec pre výpočet povrchu nie je celkom správny, pretože keby sme doložili x=r tak by vyšla derivácia nekonečno, ale na odvodenie to stačí.
Vzorec pre výpočet povrchu nie je celkom správny, pretože keby sme doložili x=r tak by vyšla derivácia nekonečno, ale na odvodenie to stačí.
Veľmi jednoducho z tohto vzorca určíme objem gule VG, keď zintegrujeme povrch gule 4πr2 podľa diferenciálu dr. Dostávame integrál![]() Pri integrácii povrchov vyzerá to ako keby sme vyťahovali hmotu gule od stredu. Na týchto príkladoch je veľmi dobre demonštrované ako sme prišli k niektorým vzorcom, ktoré sme sa v škole učili ale ako na to prišli matematici, to už nám nepovedali.
Pri integrácii povrchov vyzerá to ako keby sme vyťahovali hmotu gule od stredu. Na týchto príkladoch je veľmi dobre demonštrované ako sme prišli k niektorým vzorcom, ktoré sme sa v škole učili ale ako na to prišli matematici, to už nám nepovedali.

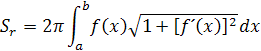





















Celá debata | RSS tejto debaty