aldebaran.pravda.sme

Trochu preskočím na dávnejšiu dobu trochu zámerne pretože chcem dokončiť matematiku. Podľa zákonov fyziky sa najlepšie vysvetľuje. Na prelome 17. a 18. Storočia anglický fyzik a matematik Isaac Newton rozšíril dovtedajšie poznatky vo fyzike kde uplatnil hmotnosť telies a ich rýchlosť pri výpočte sily a práce. Hmotnosť nie váha. Kilogram na Mesiaci váži menej ako na Zemi, ale stále to bude kilogram. Hmotnosť je hustota hmoty v objeme, kilogram pary bude mať menší objem ako kilogram vody. Pri pohybe telies sa prejavuje vlastnosť hmoty, zotrvačnosť. Newton zaviedol aj hodnotu hybnosť p, je to násobok rýchlosti v a hmotnosti m. Vzorec je p=mv.

Keď sa teleso pohybuje v priestore kde ho nič nebrzdí napr. trenie s rovnomernou priamočiarou rýchlosťou, tak sa pohybuje zotrvačnosťou. Vtedy na teleso nepôsobí žiadna sila. Takýto prípad môžeme nasimulovať napr. na naklonenej rovine, kde gravitácia eliminuje trenie. Z praxe taký prípad sú družice, odstredivá sila družice pri obehu zeme je rovnaká ako gravitačná sila. Sily sa navzájom vynulujú. O tom hovorí prvý Newtonov zákon zotrvačnosti – teleso je v pokoji alebo v rovnomernom priamočiarom pohybe keď na neho nepôsobia nijaké sily.

Majme teleso ktoré sa pohybuje rovnomernou rýchlosťou tak, že nepôsobia na neho iné sily. Keď teleso narazí na nejakú prekážku, jeho rýchlosť klesne, nastáva záporná zmena rýchlosti tzn. že zrýchlenie bude záporné. Tým pádom začína na teleso pôsobiť sila. Keď budeme pôsobiť silou na teleso tak, že sa bude pohybovať rovnomernou rýchlosťou, znamená že tam pôsobia sily ktoré brzdia pohyb. Taká sila môže byť napr. trenie. Vtedy musíme počítať s hodnotami ktoré nahrádzajú zrýchlenie napr. súčiniteľ trenia. Jednotku sily musíme odvodiť z rovnomerného zrýchlenia, podľa vzorcov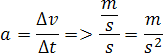Keď teleso s hmotnosťou 1kg má zrýchlenie 1m/s², tak bude na neho pôsobiť sila 1N, „Sila F sa udáva v Newtonoch N. Sila pôsobí na teleso tak, že ho deformuje. Silomer je založený na tom princípe, že meriame deformáciu telesa napr. natiahnutie pružiny. Keď na nejakú guľu zavesím pružinu tak nemusím merať deformáciu gule ale pôsobenie na inú hmotu v našom prípade pružinu, pretože guľa je príliš pevná. V skutočnosti ale nemeriame silu ale deformáciu ktorú spôsobila sila po dráhe, prácu W. Práca je pôsobenie sily po dráhe W=Fs. Ale problém je, že počítame iba s rovnomernými hodnotami. Čo keď sa na jednotlivých úsekoch dráhy bude meniť sila. Musíme si odvodiť nejako matematicky okamžitú hodnotu pomocou integrálov. Zápis pre prácu  medzi dvoma bodmi na dráhe môžeme zapísať W=

Problém je že potrebujeme poznať podľa akej funkcie sa bude meniť sila. Prácu tak musíme pracne počítať keď nepoznáme zmeny sily. Schopnosť konať prácu má každé pohybujúce teleso. Táto schopnosť sa nazýva kinetická energia. zlomok v poslednom integrále si môže upraviť podľa vzorca a dostaneme člen vdv Pre pohybujúce teleso, keď zanedbáme vonkajšie sily napr. trenie môžeme určiť koľko práce spotrebujeme na zvýšenie rýchlostivyriešením integrálov dostaneme vzorecKeď budeme uvažovať, že pohybujúce teleso má schopnosť konať prácu, kinetickú energiu E_k. tak rozdiel kinetických energii nám dáva prácu ktorú vykonalo teleso a podľa toho môžeme odvodiť aj vzorec pre kinetickú energiuVidíme, že kinetická energia je závislá aj na hmotnosti. Druhý Newtonov zákon hovorí, že časová zmena hybnosti telesa sa rovná pôsobiacej sile. Tento zákon sa nazýva zákon sily

Vrátim sa k hmotnosti. Už Galileo Galilei pozoroval, že telesa z rôznou hmotnosťou padajú rovnakou rýchlosťou. V obyčajnom prostredí pôsobí na telesá trenie vzduchu. Súčiniteľ trenia vzduchu závisí aj od hmotnosti telies. Preto sa zdá, že telesa padajú nerovnomerne. Ale prečo padajú nerovnomerne. Voľný pád je rovnomerne zrýchlený pohyb.   Zotrvačná sila pôsobí opačne sila ktorá vyvolala zrýchlenie telesa.Z toho môžeme určiť, že na padajúce teleso pôsobí určité gravitačné zrýchlenie g. Vychádzame z vzorca pre silu

Newton uvažoval, že na padajúce teleso musí pôsobiť ešte jedná sila ktorá zabraňuje letieť ťažšiemu telesu rýchlejšie. Tie sily musia začínať spolu aj končiť spolu. jedná sila je v smere pohybu a druhá taká istá fiktívna sila má opačný smer. Na telesá ktoré pôsobia silou voči sebe tak každé teleso pôsobí na druhé takou istou silou. môžeme si to predstaviť, keď dáme silomer na teleso ktoré stojí na zemi, tak silomer ukáže určitú hodnotu aj smer sily. Keď silomer obrátime tak silomer ukáže takú istú výchylku ale sila bude mať opačný smer. Tento tretí Newtonov zákon sa volá zákon akcie a reakcie.

Chcel som do spolitizovaných blogov napísať niečo kde by sa nemuselo nikomu nadávať, aj keď je to článok nezaujímavý. V budúcom blogu napíšem niečo o gravitácii