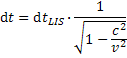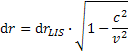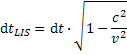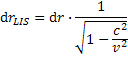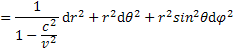Pád do čiernej diery
10. januára 2019,
aldebaran,
Nezaradené
Schwarcszchild vyriešil na podkladoch ktoré mal od Einsteina aj ako bude padať fotón alebo častica do čiernej diery. Častica bude padať voľným pádom a na horizonte udalosti by mala mať rýchlosť svetla vo vákuu, podľa normálneho vysvetlenia voľného pádu z nekonečna by pri dopade mala rýchlosť svetla. Technický môžeme na najvyššiu rýchlosť urýchliť protón. Elektrón je síce menšia častica ale vyžaruje silné brzdné žiarenie väčšie ako protón. Neutrón sa časom rozpadne ale pri jeho rozpade vznikne častica neutríno. Nemá brzdné žiarenie nemá elektrický náboj, dobre prechádza cez hmotu, reaguje iba na tzv. slabé elektrické sily. Nejdem vysvetľovať čo to je. V CERNE bola dokonca nameraná jeho rýchlosť vyššia ako rýchlosť svetla vo vákuu ale nakoniec vysvitlo, že to bola obyčajná porucha na svetelnom kábli ktorý zabezpečoval synchronizáciu medzi zdrojom neutrín a detektorom neutrín. Rozdiel medzi fotónom a neutrínom je v tom, že neutríno gravitácia urýchľuje ale fotón nezrýchľuje. Tým, že zrýchlenie častice vzrastá exponenciálne, tak na ňu bude pôsobiť extrémne preťaženie. Podľa mňa hmota sa veľmi nepriblíži k horizontu udalosti ale sa rozpadne na fotóny. Aj neutríno tým že dostáva kinetickú energiu zvyšuje svoju hmotnosť a začína kmitať resp. sú zaznamenané také balíky neutrín. Toto preťaženie môže deformovať každú jednu časticu. Fotón síce neurýchli gravitácia ale dodá mu energiu. Jeho vlnová dĺžka sa skráti. Schwarczchild neutrína nepoznal ale uvažoval o sústave, môžeme si to predstaviť ako nejaký bod ktorý padá do čiernej diery. Na sústave ktorá bude padať do čiernej diery sa budú prejavovať relativistické účinky, vzdialenosti pozorované z vonku sa budú skracovať a časy sa budú na sústave predlžovať. Fotón nezrýchľuje ale dostane energiu od gravitácie. Tým, že na neho pôsobí tak časť energie mu odovzdáva. Je to niečo podobné ako voľný pád. Teleso voľným pádom zrýchľuje tým sa jeho kinetická energia zvyšuje.
Prečo sa bude plynutie času predlžovať, dilatáciu času a pozorované dĺžky sa budú skracovať, kotrakciu dĺžok prejavovať pri rýchlostiach blízkych rýchlosti svetla vo vákuu, Einstein to vysvetľoval na vlaku ktorý by išiel rýchlosťou blízkej rýchlosti svetla a naraz by na začiatok vlaku a na koniec vlaku udreli blesky. Na začiatku a na konci vlaku vzniknú elektromagnetické vlny ktoré sa budú šíriť iba z toho jedného bodu na dráhe je jedno či sa vlak pohne. Aj keď posledný vagón keď sa pohne elektromagnetická vlna sa nebude šíriť z konca vagóna ale z bodu na dráhe kde blesk vagón zasiahol. Na začiatku vlaku to bude opačne. Detektor elektromagnetických vĺn ktorý je umiestnený v strede vlaku zaznamená dve elektromagnetické vlny v rozdielnom čase. Elektromagnetická vlna ktorá príde od konca vlaku dôjde neskôr pretože detektor sa vzdialil od bodu kde vznikla elektromagnetická vlna. Ale elektromagnetická vlna zo začiatku vlaku príde skôr pretože detektor sa priblížil k bodu kde vznikla elektromagnetická vlna, zaznamenali by sme skrátenie dĺžky. Čo je na tom čudné. Ale predstavme, že by sme ten hypoteticky vlak zmenšovali tak aby bol iba jeden bod. Tie isté efekty by sa prejavili na tom bode. Matematicky dilatáciu času a kontrakcie dĺžok som odvodil v predchadzajúcich blogoch http://aldebaran.blog.pravda.sk/2017/12/05/nieco-o-svetle-case-a-dlzke/ a http://aldebaran.blog.pravda.sk/2017/12/14/vzdialenosti-a-rychlosti/. Pre predĺženie plynutia času je vzorec 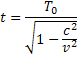 t je výsledný čas, T0 je čas ktorý zaznamenávame pri nulovej rýchlosti, v je rovnomerná rýchlosť na ktorú sme teleso urýchlili a c je rýchlosť svetla vo vákuu. Pre skrátenie, kontrakciu dĺžky platí vzťah
t je výsledný čas, T0 je čas ktorý zaznamenávame pri nulovej rýchlosti, v je rovnomerná rýchlosť na ktorú sme teleso urýchlili a c je rýchlosť svetla vo vákuu. Pre skrátenie, kontrakciu dĺžky platí vzťah 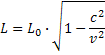 L je dĺžka, ktorú pozorujeme keď je teleso v pohybe alebo my sme v pohybe a pozorujeme teleso ktoré stojí. L0 je skutočná dĺžka telesa. Potom zmeny času dt a dráhy dr budú pre padajúcu sústavu rozdielne. Padajúcu sústavu označil Schwarczchlid symbolom LIS. Podľa toho sú zmeny plynutia času dt
L je dĺžka, ktorú pozorujeme keď je teleso v pohybe alebo my sme v pohybe a pozorujeme teleso ktoré stojí. L0 je skutočná dĺžka telesa. Potom zmeny času dt a dráhy dr budú pre padajúcu sústavu rozdielne. Padajúcu sústavu označil Schwarczchlid symbolom LIS. Podľa toho sú zmeny plynutia času dt
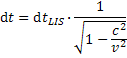
a zmeny skrátenia pozorovaných dĺžok dr ktoré registruje pozorovateľ na padajúcej sústave 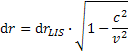
Ale na v rovnici musíme požiť čas dtLIS a dĺžku drLIS u. Rovnice pre čas dtLIS je
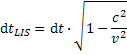 a pre dĺžku drLIS je
a pre dĺžku drLIS je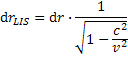
Znamená to, zmeny dráhy dr sú oveľa väčšie ako pozorujeme v padajúcej sústave, pretože sústava zrýchľuje. Zmena času sa bude skracovať pretože rýchlosť sústavy bude stúpať a rozdiel dráhy c·t-r sa bude zmenšovať. Rýchlosť sústavy sa bude približovať rýchlosti svetla. Keď to vložíme do rovnice pre sférické súradnice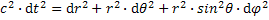
dostaneme rovnicu ktorá na ľavej strane bude vyzerať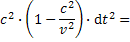
,a na pravej strane rovnice 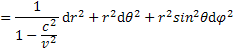
Na prvý poľad to vyzerá zložite ale v skutočnosti je to Pytagorova veta na súčet štvorcov. S tejto rovnice vychádzal Schwarczchild na zostrojenie svojej metriky. Metrika je ľudovo povedané matematicky nástroj podľa ktorého môžeme počítať vzdialenosti. Myslel som, že to dokončím v tomto blogu ale bolo by to zbytočne veľa vzorcov naraz.
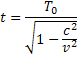 t je výsledný čas, T0 je čas ktorý zaznamenávame pri nulovej rýchlosti, v je rovnomerná rýchlosť na ktorú sme teleso urýchlili a c je rýchlosť svetla vo vákuu. Pre skrátenie, kontrakciu dĺžky platí vzťah
t je výsledný čas, T0 je čas ktorý zaznamenávame pri nulovej rýchlosti, v je rovnomerná rýchlosť na ktorú sme teleso urýchlili a c je rýchlosť svetla vo vákuu. Pre skrátenie, kontrakciu dĺžky platí vzťah 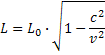 L je dĺžka, ktorú pozorujeme keď je teleso v pohybe alebo my sme v pohybe a pozorujeme teleso ktoré stojí. L0 je skutočná dĺžka telesa. Potom zmeny času dt a dráhy dr budú pre padajúcu sústavu rozdielne. Padajúcu sústavu označil Schwarczchlid symbolom LIS. Podľa toho sú zmeny plynutia času dt
L je dĺžka, ktorú pozorujeme keď je teleso v pohybe alebo my sme v pohybe a pozorujeme teleso ktoré stojí. L0 je skutočná dĺžka telesa. Potom zmeny času dt a dráhy dr budú pre padajúcu sústavu rozdielne. Padajúcu sústavu označil Schwarczchlid symbolom LIS. Podľa toho sú zmeny plynutia času dt