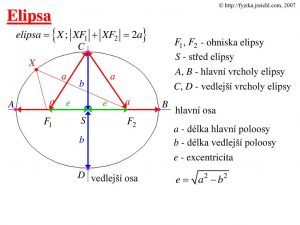
© Elipsa. , – ohniska elipsy. C. S – střed elipsy. X. A, B – hlavní vrcholy elipsy. a. a. b. C, D – vedlejší vrcholy elipsy. a. e. e. a. A. B. hlavní osa. S. a – délka hlavní poloosy. b. b – délka vedlejší poloosy. e – excentricita. D. vedlejší osa.
Trochu neskoro reagujem na článok o elipse, ktorý písal pán Bednár. V jeho blogu je uvedené, že veľkosť obvodu elipsy sa nedá vypočítať. Skutočne je to pravda, skúsim to vysvetliť. Keď uvážime fakt, že π má nekonečne veľa číslic za desatinnou čiarkou tak ani veľkosť kružnice sa presne nedá vypočítať. Najprv vysvetlím niečo o elipse. Elipsa je v podstate roztiahnutá kružnica, kde polomer kružnice sa rozdelí na dve ohniská. Parametre elipsy sú popísaná na spodnom obrázku

© Elipsa. , – ohniska elipsy. C. S – střed elipsy. X. A, B – hlavní vrcholy elipsy. a. a. b. C, D – vedlejší vrcholy elipsy. a. e. e. a. A. B. hlavní osa. S. a – délka hlavní poloosy. b. b – délka vedlejší poloosy. e – excentricita. D. vedlejší osa.
Vzdialenosť ohnísk od stredu elipsy je excentrita
Veľmi dôležitá je číselná excentrita ε ktorá udáva sploštenosť elipsy. Vzorec je
Elipsu si môžeme predstaviť v súradnicovej sústave kde na osi x sú poloosi a a na súradnici y sú poloosi b. Vzdialenosti od bodu na elipse k obidvom ohniskám sa nazývajú sprievodiče. Súčet dĺžok sprievodičov bude vždy 2a. sprievodiče tvoria trojuholník ktorý môžeme rozdeliť na dva pravouhlé. Podľa Pytagorovej vety dostávame rovnicu
Bod X je udaný súradnicami x y na osiach. Keď je bod X v bode C alebo D tak x=0 a y=b. Ak je v bode B alebo A tak je y=0 a x=a. Vyplýva to vlastne výpočtu excentrity e, súčet dĺžky sprievodičov je vždy 2a. Platí to vtedy keď je poloos a väčšiu ako b. Pri opačnom garde sa iba vymenia poloosi a za b vo výpočte excentrity a súčet bude 2b. Keď poznáme parametre a b, zvolíme x a cheli by sme vedieť súradnicu y musíme si rovnicu upraviť na
Z tejto rovnice asi po desiatich riadkoch dostaneme základnú rovnicu elipsy![]()
Keďže sa bavíme o obvode elipsy čo je krivka, tak vysvetlím princíp výpočtu dĺžky krivky ktorá má súradnice na osiach x y. Na osi x máme dva body medzi ktorými potrebujeme určiť dĺžku krivky. Aby sme si pomohli rozsekáme ten úsek na osi x na malé rovnaké časti Δx a na osy y by sme podľa bodov na krivke určili vzdialenosti Δy. Vzniká nám pravouhlý trojuholník kde prepona bude malá časť krivky Δs . Podľa Pytagorovej vety dostaneme vzorec
Súčtom všetkých Δs by sme získali približnú veľkosť krivky. Čím menšia bude vzdialenosť Δx, tým presnejší výsledok dostaneme. Môžeme urobiť taký trik že budeme uvažovať zmeny elementárne a nahradíme ich diferenciálmi ds, dx a dy. Potom môžeme rozpísať rovnicu
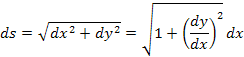 dy/dx je derivácia funkcie y´ podľa vzorca
dy/dx je derivácia funkcie y´ podľa vzorca
Každá krivka v súradnicovej sústave má nejakú funkciu, ktorú môžeme derivovať, potom sa vzorec zmení na
Integráciou dostaneme rovnicu, kde hľadaná vzdialenosť je medzi bodmi x1 x2
Vzorec pre integrál dostaneme podľa funkcie krivky. Výsledný integrál vypočítame podľa vzorca
Diferenciál dostaneme podľa vzorca
![]() Elipsa je krivka ktorú môžeme považovať, že vychádza z kružnice. Kružnica má rovnicu
Elipsa je krivka ktorú môžeme považovať, že vychádza z kružnice. Kružnica má rovnicu
![]()
Vzdialenosť bodu A od stredu kružnice je polomer r ktorý tvorí preponu pravouhlého trojuholníka na osiach x y.
Pre presnejšie vyjadrenie môžeme si pomôcť s kružnicou ktorá bude mať polomer 1 podľa obrázka
a potom vzdialenosti x y môžeme prepísať pomocou sínusu a kosínusu podľa rovníc![]()
Derivácie kosínusu a sínusu sú![]() Dosadením do vzorca pre ds musíme vložiť miesto dx element uhlu diferenciál dφ a dostaneme vzorec
Dosadením do vzorca pre ds musíme vložiť miesto dx element uhlu diferenciál dφ a dostaneme vzorec
![]() Veľkosť oblúka počítame integáciou podľa vzorca
Veľkosť oblúka počítame integáciou podľa vzorca
Uhly α β udávajú ako bude uhol φ natočený v kružnici. Pri uhle α oblúk začína a pri uhle β . Výpočet integrálu oblúka kružnice má jednoduchý vzorec pretože pod odmocninou je vždy 1 integrujeme iba dφ
Taký výpočet oblúka nemá praktický význam ale napr. odvodení povrchu gule ho musíme použiť. Ja som ho použil iba na ukážku. Uhly sa udávajú v radiánoch, násobkoch π, celá kružnica je ako vieme 2π. Veľkosť oblúka získame násobením radiánu polomerom. Pre elipsu z toho bude platiť následovné rovnice![]()
Keď vložíme derivácie podobne ako pri kružnici dostávame vzorec pre diferenciál![]()
Podľa vzorca cos2=1-sin2môžeme upraviťrovnicu![]()
Ďalšou úpravou získame konečný vzorec pre diferenciál elipsy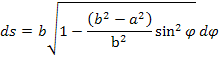
Keby sme chceli vypočítať obvod elipsy C musíme vypočítať dĺžku kvadrantu elipsy s podľa integrálu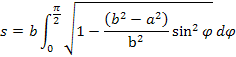
Toto je odvodenie pre b>a. Viac sa požíva opačné garde pretože, číselná excentrita ε odvodená tak, že poloos a je väčšia ako poloos b. Vo výsledku iba vymeníme a za b. Pod odmocninou máme v podstate cos2 a integrovaním kosínusu dostávame sínus. Pri kvadrante sa sínus rovná 1 ale to znamená, že, máme dve premenné integrovať môžeme iba jednu. Tento integrál sa volá úplný eliptický integrál, nedá jednoducho riešiť. Tento integrál sa niekedy označuje E(dφ), z toho vyplýva že obvod elipsy je C=4E(dφ)
Keď si uvedomíme, že elipsa je sploštená kružnica, tak môžeme uvažovať, že obvod elipsy bude menší ako obvod kružnice s polomerom a, ale väčší ako obvod kružnice s polomerom b. Poznáme mieru sploštenia, číselnú excentritu ε tak môžeme navrhnúť nejaký algoritmus kde postupným zmenšovaním obvodu kružnice s polomerom a sa budeme približovať k obvodu elipsy. Integrál sa počíta podľa nekonečného rádu zo vzorca
Čím presnejší výpočet potrebujeme tým ten rad musí byť väčší. V praxi nepotrebujeme počítať veľmi presne napr. na výpočet kružnice stačí 3,14. Je veľa vzorcov na výpočet veľkosti obvodu elipsy, ale každý má určitú presnosť.
Budem rád keď si to niekto aj prečíta