V predchádzajúcom blogu https://aldebaran.blog.pravda.sk/2024/12/04/nieco-o-hyperbole/ som písal, že polovica hyperbolického uhla je určená plochou S
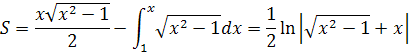
Na vysvetlenie je potrebné odvodiť integrál, ktorý môžeme prepísať na neurčitý integrál pretože výsledok bude rovnaký
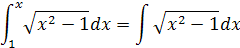
Integrály pod odmocninou sa priamo nedajú vypočítať, preto ich musíme modifikovať tak aby sa dali integrovať. Pre x použijeme obrátenú hodnotu kosínus θ, pretože kosínus v nule je 1tým pádom hodnota pod odmocninou nebude nikdy záporná
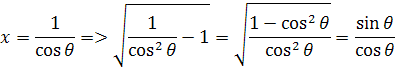
Musíme vyjadriť aj dx pomocou derivácie
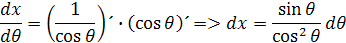
Keď hodnoty vložíme do integrálu a úpravou získame rovnicu
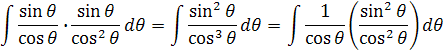
Rozpísaním dostaneme výslednú rovnicu
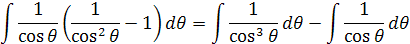
Túto rovnicu si môžeme prispôsobiť na tvar
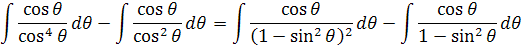
Tieto integrály sa dajú vypočítať pár riadkami ale je to jednoduché pre toho kto vie integrovať. Ja som vybral na prvý pohľad zložité odvodenie ale v podstate je to deviatacká matematika. Znovu nahradíme sín θ = y. pre diferenciál dostávame odvodenie
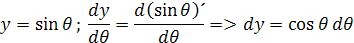
Vložíme do rovnice a dostaneme integrál
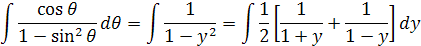
Úpravou tohto integrálu dostaneme vyriešenie druhého integrálu. Hodnoty v prirodzenom logaritme môže byť iba kladné, pretože logaritmus záporného čísla nejestvuje, preto musíme počítať hodnoty v absolútnych hodnotách Integrál 1/x je ln x z toho 1/y+1 = ln |y+1|
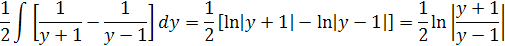
Podobne môžeme vyriešiť aj prvý integrál
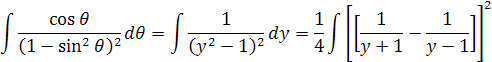
Rozpíšem hodnoty v zátvorke
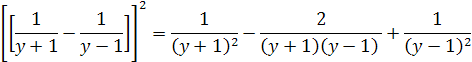
Z toho vychádza integrál
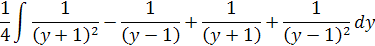
Vyriešením podľa integrálnych vzorcov dostaneme výsledok. Integrál 1/x2=-1/x podľa toho je 1/(y+1)2=-1/(y+1)
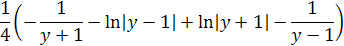
Odčítanie logaritmov je delenie dostávame ďalšiu úpravu
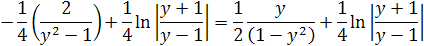
Odčítaním výsledkov integrálov dostaneme rovnicu
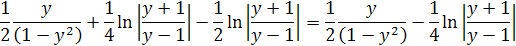
Vložením hodnôt sin θ a cos θ dostaneme rovnicu prvý integrál
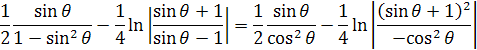
Záporné znamienko pred cos2 θ vypadne, pretože by sme dostali záporné číslo a odstránením exponentu 2 sa zmení pred ln 1/4 na 1/2. Odčítaním výsledkov integrálov dostaneme výsledok

Keď do vložíme pôvodné hodnoty dostaneme vzorce
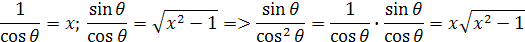
Z toho dostaneme výslednú rovnicu
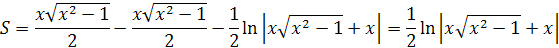
Takto sme sa dopracovali výsledku. Článok z matematiky je v terajšej dobe veľmi nezaujímavá téma. Dúfam, že si článok niekto aj prečíta



















Na Járaya je to príliš konkrétne, on sa vyžíva... ...
ano historia matematiky je tiež taký román.... ...
no jaray nie som ale počiatok týchto blogov je... ...
Akonáhle je texte viac písmen, než číslic,... ...
akože v týchto veciach sa nevyznám, ale mal... ...
Celá debata | RSS tejto debaty