aldebaran.pravda.sme

Nemecký astronóm Johannes Kepler medzi rokmi 1609 až 1619 objavil 3 základné zákony pohybov planét. 1. zákon hovorí „planéty sa pohybujú okolo Slnka po elipsách a Slnko je v ohnisku elipsy“, 2. zákon hovorí  „sprievodič (spojnica Slnka a planéty) opíše za rovnaký čas vždy rovnakú plochu“ a 3. zákon hovorí „pomery  druhých mocnín času obežných dôb dvoch planét  (T₁)²/(T₂)²  je rovnaký ako ich pomer tretích mocnín strednej vzdialenosti od Slnka, (polomer hlavnej osi elipsy  (a₁)²/(a₂)³. Kepler nemohol poznať vzdialenosti planét od Slnka, ale zvolil si za základ strednú vzdialenosť zeme od slnka. Je to jedna  astronomická jednotka 1AU. Pre ostatné planéty je vzdialenosť a násobok 1AU, to mohol odmerať. Za čas T si zvolil dobu za koľko pozemských dni planéta obehne okolo Slnka. Jeho teleskop bol veľmi nedokonalý, preto mu merania trvali tak dlho. Dole je obrázok dráhy dvoch planét, kde sú vyobrazené obežné dráhy a poloosi a₁ a a₂.

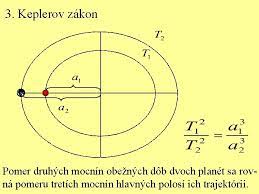
Z rovnice ktorá je na obrázku môžeme odvodiť konštantu C

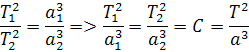
Z tejto rovnice môžeme odvodi T² podľa vzorca

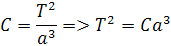
Newton na základe Keplerovych zákonov si uvedomil, že jeho pohybové zákony sa dajú aplikovať aj na pohyby planét, Pretože medzi gravitáciou Slnka a planétami musia pôsobiť určité sily ktoré udržujú planéty vo svojich dráhach. Planéty obiehajú okolo Slnka po elipsách, kde Slnko je v ohnisku elipsy. Pôsobí na nich gravitačná sila Slnka. Aby sa planéty udržiavali vo svojich dráhach, tak musia mať určitú odstredivú silu, aby ich gravitácia Slnka nepritiahla. Sila vzniká keď má teleso nejaké zrýchlenie, alebo keď je rýchlosť konštantná ale teleso sa nepohybuje priamočiaro. Zrýchlenie planéty môžeme odvodiť z uhlovej rýchlosti telesa po kruhovej dráhe, kde namiesto vzdialenosti a použijeme vo vzorci vzdialenosť r. Budeme uvažovať, že planéty obiehajú rovnomernou rýchlosťou okolo stredu vo vzdialenosti r. Pri rovnomernej rýchlosti v prejde bod na dráhe s za čas t vzorec je v=s/v. keď je dráha rovná tak pri rovnomernej rýchlosti neexistuje zrýchlenie. ale keby sme otáčali nejakou hmotnosťou rovnomerne dookala tak bude na ňu pôsobiť odstredivá sila. Znamená to že pri rovnomernej kruhovej rýchlosti existuje zrýchlenie. Rovnomerná kruhová rýchlosť má vzorec v_o=2πr/T. Dráha je s=2πr a T je doba otočenia. Konštantu C môžeme rozpísať podľa r. Zt oho nám vychádza vzorec

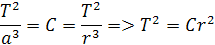
Z toho môžeme odvodiť vzorec pre dostredivé zrýchlenie zrýchlenie a_d

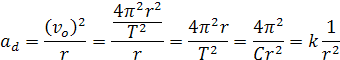
Z toho vychádza, že teleso o hmotnosti m vo vzdialenosti ťažiska r má zýchlenie  k/r² a vytvára odstredivú silu F=mk/r². Slnko planétu priťahuje takou istou silou F´ . Hmotnosť Slnka je M ale konštanta je k´ . Porovnaním týchto dvoch rovníc, môžeme odvodiť konštantu G

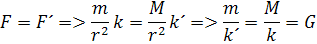
Rovnica hovorí, vo vzdialenosti ťažisk r má planéta odstredivú silu F ale rovnakou silou F´  , priťahuje Slnko planétu vo vzdialenosti r. Pretože pomery hmotností s opačnými konštantami sú rovnaké, preto si môžeme odvodiť gravitačnú konštantu G. Aby sme vyradili konštanty k a k´ v rovnici pre rovnosť síl vynásobíme pravú stranu rovnice G². Rozpísaním pre G² dostávame vzorec

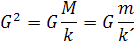
Vložením do rovnice dostaneme odvodenie vzorca pre silu

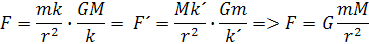
F je sila ktorou sa dve telesá priťahujú, G je gravitačná konštanta, M je väčšia hmotnosť telesa ktoré priťahuje, m je hmotnosť priťahovaného telesa a r je vzdialenosť ťažísk telies. Výsledný vzorec je

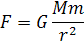
Z  hmotností M  a m a zrýchlenia a_d=4π²/T² si môžeme rozpísaním síl F=F´ si môžeme odvodiť rovnicu

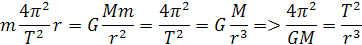
Obrátením vzorca a vložením miesto r, a musíme hmotnosť M zväčšiť o hmotnosť planéty m. Z toho dostávame rovnicu

Z týchto rovníc keď poznáme hmotnosti M a m a vzdialenosť a môžeme vypočítať čas obehu planéty T. Keď budeme poznať a čas T a hmotnosť planéty bude zanedbateľná môžeme vypočítať hmotnosť M.