Gravitácia čiernej diery je taká silná na povrchu resp. horizonte udalosti, že pohltí aj svetlo ktoré sa nachádza v blízkosti čiernej diery a vzdialenejšie svetlo ohne. Preto čiernu dieru vidíme ako gravitačnú šošovku. Čierna bodka okolo ktorej žiary svetlo. Ale väčšinou to svetlo môžu vidieť iba družice pretože je v gama spektre. Svetlo ale padá trochu ináč do čiernej diery ako telesá. Fotóny majú konštantnú rýchlosť vo vákuu. Keď narazia na hmotu tak predajú jej svoju energiu a zaniknú v nejakej forme alebo zmenia svoju energiu a pokračujú v putovaní, zrkadlá. Gravitácia padajúcemu telesu pridáva kinetickú energiu, zvyšuje sa rýchlosť jeho pádu. Fotóny rýchlosť nezvyšujú ale gravitácia pôsobí nich tak, že ohýba ich dráhu letu. Fotóny nemajú odstredivé sily preto ich gravitácia bude vždy ohýbať k horizontu udalosti ale fotóny sa budú snažiť z tejto pasci uniknúť. Preto do čiernej diery nebudú padať ako telesá. V určitej vzdialenosti od horizontu udalosti sa dráhy fotónov budú ohýbať tak že budú padať ako v lieviku do gravitačného poľa čiernej diery. Dole je obrázok kde je znázornené po akej ploche budú padať fotóny do čiernej diery. Ich dráha bude vyzerať ako šroubovica.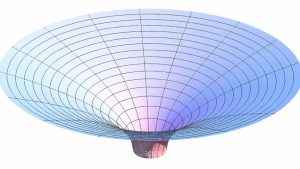
Koniec toho lievika je okolo stredu čiernej diery ale je ďalej od horizontu udalosti. Spodný obrázok ukazuje ako sa budú telesa správať v okolí čiernej diery. Zelené teleso má dostatočnú rýchlosť na to aby gravitácia čiernej diery jeho dráhu iba zahla. Modré teleso rotuje okolo čiernej diery. Musí mať takú veľkú obehovú rýchlosť aby sa jeho odstredivé sily vyrovnali priťažlivým gravitačným silám v danej vzdialenosti od stredu čiernej diery. Červené teleso nemá dostatok energie aby mohlo rotovať okolo horizontu udalostí ale padá dovnútra čiernej diery. Na horizont udalosti sa ale nedostane pretože už pred horizontom udalosti je jedna sféra kde môžu obiehať iba fotóny a tie majú rýchlosť svetla. Teleso dosiahne takú relativistickú hmotnosť, že sa musí v určitej dráhe zmeniť na fotóny. Keby letelo rýchlosťou svetla tak jeho energia by musela byť nekonečná.
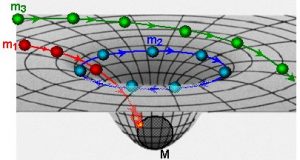 Druhý najväčší parameter ktorý charakterizuje jej veľkosť čiernej diery je tzv. fotónová sféra. Je to obežná dráha okolo stredu čiernej diery kde môžu obiehať iba fotóny. na prvom obrázku si ju môžeme predstaviť na spodku toho gravitačného lievika. Fotón prenáša informáciu pomocou svojej frekvencie resp. vlnovej dĺžky. Pretože fotón sa na povrchu čiernej diery stratí tak hovoríme o povrchu čiernej diery ako o horizonte udalostí. Udalosť je informácia.
Druhý najväčší parameter ktorý charakterizuje jej veľkosť čiernej diery je tzv. fotónová sféra. Je to obežná dráha okolo stredu čiernej diery kde môžu obiehať iba fotóny. na prvom obrázku si ju môžeme predstaviť na spodku toho gravitačného lievika. Fotón prenáša informáciu pomocou svojej frekvencie resp. vlnovej dĺžky. Pretože fotón sa na povrchu čiernej diery stratí tak hovoríme o povrchu čiernej diery ako o horizonte udalostí. Udalosť je informácia.
Schwarczchild vychádzal pre výpočtu dráhy pádu do čiernej diery zo sférickej metriky ktorá zohladňovala relativistické účinky telesa, pretože pri páde telesa do čiernej diery bude jeho rýchlosť voľného pádu blízka rýchlosti svetla. Ale na rozdiel od klasickej teleso padá do stredu súradníc. Stred súradníc nie je bod ale polomer čiernej diery. Dokonca nemohol byť ani na horizonte udalosti pretože tam by fotón už neexistoval. Musí to byť ešte jedna sféra kde by mohol obiehať iba fotón. Hmota sa tam dostať nemôže pretože by musela mať nekonečnú energiu ale fotón môže, pretože najvyššia energia fotónu je Planckova energia. O Planckovej energii som písal na blogu, http://aldebaran.blog.pravda.sk/2018/10/23/planckove-hodnoty/.
Nad horizontom udalosti sú obehové rýchlosti menšie ako rýchlosti svetla vo vákuu. Porovnaním polomeru horizontu rs a polomeru r, ktorý je väčší ako Schwarczchildov polomer, udáva nám pomer c2/v2. v je úniková rýchlosť pre danú vzdialenosť, r je daný polomer. Porovnaním dostaneme rovnicu
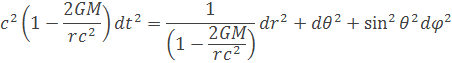
Keď rovnicu vydelíme r2 a derivujeme podľa dt dostaneme rovnicu
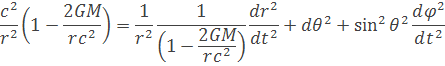
Fotónova sféra má polomer rf väčší ako Schwarzildov polomer rs. Aby sa otáčali fotóny okolo čiernej diery musí byť uhol θ kolmy na os otáčania. Nemôžu byť žiadne zmeny tzn. že difrenciály aj deriváca majú nulové hodnoty ani uhlové zrýchlenie. do rovnice vložíme tieto hodnoty
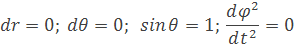
dostaneme rovnícu
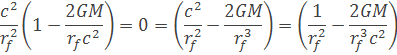
úpravou rovnice dostávame rovnicu kde môžeme derivovať polomer rf
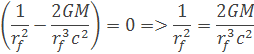
po derivácii vychádza rovnica
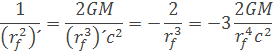
rovnicu vykrátime a môžeme si z nej odvodiť polomer fotónovej sféry rf
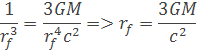
polomer fotónovej sféry je 1,5 násobne väčší ako Schwartzildov polomer. Aby som mohol vysvetliť resp. odvodiť polomer fotónovej sféry musel som vysvetliť suradnice. Nabudúce dokončím blog o fotónovej sfére



















som rád, že si to prečítate. myslel som že ...
Ďakujem za zrozumitelne písané vzorce. Nie ...
Celá debata | RSS tejto debaty