Keď je na súradnicovej osi x je premenná mocnina ktorou umocňujem základ a tak dostanem exponenciálnu funkciu y=ax. Dole je graf funkcii kde čiarkovaná čierna krivka ma základ 4, modrá krivka ma základ e, čierna bodkovaná ma základ 2 a červená čiara je dotyčnica krivky funkcie ex v bode x=0.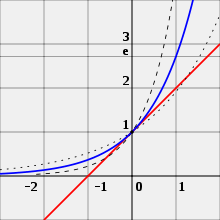
Pri skúmaní mocnín našiel škotsky matematik John Napier zaujímavú súvislosť pri porovnavaní zmeny funkcii ax medzi základmi 3 a 2. Na osy x určíme zmenu dva body x a x2=x+Δx. Za Δx si zvolíme, nejaké malé číslo. Na osi y dostaneme zmenu Δy=y2 -y1. Δx a Δy sú strany pravouhlého trojuholníka. Pomer Δy/Δx tangens uhla prepony ktorý zviera s osou x. Zaujímavosťou je, že pri základe a=3 má tangens väčšiu hodnotu ako y2, ale pri a=2 je hodnota tangensu menšia ako y2. Zostrojím niekolko tabuliek pre názornosť podľa vzorca
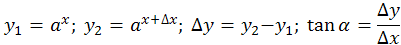
a=3, Δx=0,1
| x | a | y1 | y2 | tan α |
| 0 | 3 | 1 | 1,116123174 | 1,16123174 |
| 1 | 3 | 3 | 3,348369522 | 3,483695221 |
| 2 | 3 | 9 | 10,04510857 | 10,45108566 |
| 3 | 3 | 27 | 30,1353257 | 31,35325699 |
| 4 | 3 | 81 | 90,4059771 | 94,05977097 |
| 5 | 3 | 243 | 271,2179313 | 282,1793129 |
| 6 | 3 | 729 | 813,6537939 | 846,5379387 |
| 7 | 3 | 2187 | 2440,961382 | 2539,613816 |
| 8 | 3 | 6561 | 7322,884145 | 7618,841448 |
| 9 | 3 | 19683 | 21968,65243 | 22856,52435 |
| 10 | 3 | 59049 | 65905,9573 | 68569,57304 |
tan α je väčší ako y2
a=2, Δx=0,1
| x | a | y1 | y2 | tan α |
| 0 | 2 | 1 | 1,071773463 | 0,717734625 |
| 1 | 2 | 2 | 2,143546925 | 1,435469251 |
| 2 | 2 | 4 | 4,28709385 | 2,870938501 |
| 3 | 2 | 8 | 8,5741877 | 5,741877003 |
| 4 | 2 | 16 | 17,1483754 | 11,48375401 |
| 5 | 2 | 32 | 34,2967508 | 22,96750801 |
| 6 | 2 | 64 | 68,5935016 | 45,93501602 |
| 7 | 2 | 128 | 137,1870032 | 91,87003205 |
| 8 | 2 | 256 | 274,3740064 | 183,7400641 |
| 9 | 2 | 512 | 548,7480128 | 367,4801282 |
| 10 | 2 | 1024 | 1097,496026 | 734,9602564 |
tan α menší ako y2
a=2,8, Δx= 0,01
| x | a | y1 | y2 | tan α |
| 0 | 2,8 | 1 | 1,010349382 | 1,034938237 |
| 1 | 2,8 | 2,8 | 2,828978271 | 2,897827063 |
| 2 | 2,8 | 7,84 | 7,921139158 | 8,113915776 |
| 3 | 2,8 | 21,952 | 22,17918964 | 22,71896417 |
| 4 | 2,8 | 61,4656 | 62,101731 | 63,61309969 |
| 5 | 2,8 | 172,10368 | 173,8848468 | 178,1166791 |
| 6 | 2,8 | 481,890304 | 486,877571 | 498,7267015 |
| 7 | 2,8 | 1349,292851 | 1363,257199 | 1396,434764 |
| 8 | 2,8 | 3778,019983 | 3817,120157 | 3910,01734 |
| 9 | 2,8 | 10578,45595 | 10687,93644 | 10948,04855 |
| 10 | 2,8 | 29619,67667 | 29926,22203 | 30654,53595 |
tan α je väčší ako y2
a=2,7, Δx= 0,01,
| x | a | y1 | y2 | tan α |
| 0 | 2,7 | 1 | 1,009982009 | 0,998200891 |
| 1 | 2,7 | 2,7 | 2,726951424 | 2,695142405 |
| 2 | 2,7 | 7,29 | 7,362768845 | 7,276884492 |
| 3 | 2,7 | 19,683 | 19,87947588 | 19,64758813 |
| 4 | 2,7 | 53,1441 | 53,67458488 | 53,04848795 |
| 5 | 2,7 | 143,48907 | 144,9213792 | 143,2309175 |
| 6 | 2,7 | 387,420489 | 391,2877238 | 386,7234772 |
| 7 | 2,7 | 1046,03532 | 1056,476854 | 1044,153388 |
| 8 | 2,7 | 2824,295365 | 2852,487506 | 2819,214148 |
| 9 | 2,7 | 7625,597485 | 7701,716267 | 7611,878201 |
| 10 | 2,7 | 20589,11321 | 20794,63392 | 20552,07114 |
tan α je menší ako y2
a=2,72, Δx =0,001,
| x | a | y1 | y2 | tan α |
| 0 | 2,72 | 1 | 1,001001133 | 1,001132679 |
| 1 | 2,72 | 2,72 | 2,722723081 | 2,723080888 |
| 2 | 2,72 | 7,3984 | 7,40580678 | 7,406780015 |
| 3 | 2,72 | 20,123648 | 20,14379444 | 20,14644164 |
| 4 | 2,72 | 54,73632256 | 54,79112088 | 54,79832127 |
| 5 | 2,72 | 148,8827974 | 149,0318488 | 149,0514338 |
| 6 | 2,72 | 404,9612088 | 405,3666287 | 405,4199001 |
| 7 | 2,72 | 1101,494488 | 1102,59723 | 1102,742128 |
| 8 | 2,72 | 2996,065007 | 2999,064466 | 2999,458589 |
| 9 | 2,72 | 8149,29682 | 8157,455347 | 8158,527361 |
| 10 | 2,72 | 22166,08735 | 22188,27855 | 22191,19442 |
tan α väčší ako y2
a=2,71, Δx=0,001,
| x | a | y1 | y2 | tan α |
| 0 | 2,71 | 1 | 1,000997446 | 0,997445753 |
| 1 | 2,71 | 2,71 | 2,712703078 | 2,703077992 |
| 2 | 2,71 | 7,3441 | 7,351425341 | 7,325341357 |
| 3 | 2,71 | 19,902511 | 19,92236268 | 19,85167508 |
| 4 | 2,71 | 53,93580481 | 53,98960285 | 53,79803946 |
| 5 | 2,71 | 146,166031 | 146,3118237 | 145,7926869 |
| 6 | 2,71 | 396,1099441 | 396,5050423 | 395,0981816 |
| 7 | 2,71 | 1073,457949 | 1074,528665 | 1070,716072 |
| 8 | 2,71 | 2909,071041 | 2911,972681 | 2901,640556 |
| 9 | 2,71 | 7883,58252 | 7891,445966 | 7863,445906 |
| 10 | 2,71 | 21364,50863 | 21385,81857 | 21309,9384 |
tan α je menší ako y2
a=2,719; Δx=0,0001
| x | a | y1 | y2 | tan α |
| 0 | 2,719 | 1 | 1,000100031 | 1,000314194 |
| 1 | 2,719 | 2,719 | 2,719271985 | 2,719854293 |
| 2 | 2,719 | 7,392961 | 7,393700528 | 7,395283822 |
| 3 | 2,719 | 20,10146096 | 20,10347174 | 20,10777671 |
| 4 | 2,719 | 54,65587235 | 54,66133965 | 54,67304488 |
| 5 | 2,719 | 148,6093169 | 148,6241825 | 148,656009 |
| 6 | 2,719 | 404,0687327 | 404,1091523 | 404,1956886 |
| 7 | 2,719 | 1098,662884 | 1098,772785 | 1099,008077 |
| 8 | 2,719 | 2987,264382 | 2987,563202 | 2988,202962 |
| 9 | 2,719 | 8122,371855 | 8123,184347 | 8124,923853 |
| 10 | 2,719 | 22084,72907 | 22086,93824 | 22091,66796 |
tan α je väčší ako y2.
a=2,718; Δx=0,0001
| x | a | y1 | y2 | tan α |
| 0 | 2,718 | 1 | 1,000099995 | 0,999946307 |
| 1 | 2,718 | 2,718 | 2,718271785 | 2,717854062 |
| 2 | 2,718 | 7,387524 | 7,388262713 | 7,387127342 |
| 3 | 2,718 | 20,07929023 | 20,08129805 | 20,07821212 |
| 4 | 2,718 | 54,57551085 | 54,58096811 | 54,57258053 |
| 5 | 2,718 | 148,3362385 | 148,3510713 | 148,3282739 |
| 6 | 2,718 | 403,1778962 | 403,2182118 | 403,1562484 |
| 7 | 2,718 | 1095,837522 | 1095,9471 | 1095,778683 |
| 8 | 2,718 | 2978,486385 | 2978,784217 | 2978,326461 |
| 9 | 2,718 | 8095,525993 | 8096,335502 | 8095,09132 |
| 10 | 2,718 | 22003,63965 | 22005,8399 | 22002,45821 |
tan α je menší ako y2.
Podľa tabuliek vidíme že medzi číslami 2,719 a 2,718 musí existovať nejaké číslo kde tan α sa bude rovnať y2. znamená to že pomer Δy/Δx sa bude rovnať elementárnym zmenám, pomerom diferenciálov dy/dx. Keď si predstavíme Δy a Δx ako strany pravouhlých trojuholníkov na krivke, tak prepony pravouhlých trojuholníkov vytvárajú kostrbatú krivku. Čím bude strana Δx menšia tým bude krivka plynulejšia. Pri elemente Δx=dy bude krivka plynulá a tan α sa bude rovnať ax. Znamená to, že tangens uhla dotyčnice kryvky sa rovná hodnote ax. Podľa grafu vidno, že v bode x=0 je uhol 45° tzn. tan α=1. Toto číslo sa nedá vypočítať, pretože je nedeliteľné a má nekonečne veľa desatinných miest. Vzorec Pre výpočet určil švajčiarský matematik Leonhard Euler, podľa neho je pomenované eulerové číslo e. Jeho približná hodnota je e=2,71828182846. Viac o ňom napíšem v druhom blogu



















@matstat3 Tiež som sa na to pýtal agentov ...
seat, ako môže niekto pracovať so zloženým ...
Niečo, čo súvisí s aplikovanou matematikou, ...
Očakávam, že sa ozve akýsi "čistý"... ...
Vždy je potrebné zodpovedať aj otázku, či ...
Celá debata | RSS tejto debaty