Tento článok je pokračovanie článkov o matematike z oblasti derivácii a integrálov. Aj keď téma je z elektrotechniky, tak na konkrétnom prípade sa dá veľmi dobre demonštrovať použitie derivácii a integrálov. Dole je nakreslený obrázok tzv. RC obvodu. Myslím, že mnoho čitateľov pracuje v oblasti elektrotechniky a rozumie tomuto obvodu. Pri výpočte okamžitých hodnôt napätia alebo prúdu, pri nabíjaní alebo vybíjaní kondenzátora cez odpor, sa počíta s časovou konštantou τ v člene (e-t/τ). Pokúsim sa to vysvetliť v blogu ako sme na ten vzorec prišli. 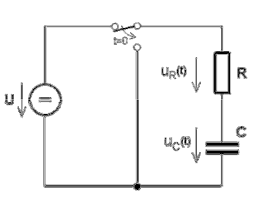 Na obrázku je odpor R a kondenzátor, resp. kapacita C. Prepínač slúži na prepínanie režimu vybíjania a nabíjania kondenzátora a U je jednosmerný zdroj napätia. Keď kondenzátor pripojíme na jednosmerné napätie sa nabije na napätie zdroja. Ale to nabíjanie neprebieha okamžite, ale po určitej dobe, teoreticky až za nekonečne dlhú dobu. Keď zapojíme nabitý kondenzátor cez odpor okamžité napätia na odpore uR a kondenzátoré uC budú rovnaké pretože platí ohmov zákon u =Ri. Napätia musíme počítať ako opačne polarizované, pretože, sú v sérii. Súčty napätia na odpore uR kondenzátore uC pretože sú rovnaké musia spĺňať rovnicu
Na obrázku je odpor R a kondenzátor, resp. kapacita C. Prepínač slúži na prepínanie režimu vybíjania a nabíjania kondenzátora a U je jednosmerný zdroj napätia. Keď kondenzátor pripojíme na jednosmerné napätie sa nabije na napätie zdroja. Ale to nabíjanie neprebieha okamžite, ale po určitej dobe, teoreticky až za nekonečne dlhú dobu. Keď zapojíme nabitý kondenzátor cez odpor okamžité napätia na odpore uR a kondenzátoré uC budú rovnaké pretože platí ohmov zákon u =Ri. Napätia musíme počítať ako opačne polarizované, pretože, sú v sérii. Súčty napätia na odpore uR kondenzátore uC pretože sú rovnaké musia spĺňať rovnicu
Vybijací prúd i=dq/dt časom klesá pretože klesá náboj qC na kapacite C a napätie uC=qC/C sa znižuje. Znamená to, že napätie na odpore uR sa bude rovnako znižovať. Podľa toho si môžeme napísať rovnicu
Vydelením rovnice R a qC a vynásobením dt dostaneme rovnicu diferenciálnu rovnicu
túto rovnicu môžeme integrovať podľa vzorcov
integrovaním tejto rovnice získame vzorec
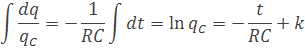
k je počiatočná podmienka, je to maximálny náboj na kondenzátore ktorý musíme napísať ako logaritmus k=ln(UC)=lnQ. Po prevedením konštanty na druhú stranu dostaneme rovnicu

Odčítanie logaritmov je delenie a z tejto rovnice môžeme odstrániť logaritmus ln podľa vzorca
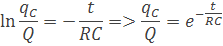
Člen RC sa nazíva časová konštanta a značí sa písmenom tau τ. Takto sme prišli k členu (e-t/τ). Z toho dostaneme výsledný vzorec pre okamžitý náboj qC v kondenzátore pri vybíjaní v čase t
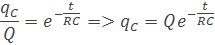
Náboj bude v kondenzátore časom pri vybíjaní klesať, tým pádom bude klesať aj napätie na kondenzátore uC. Vzorce sú
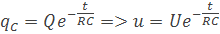
Keď budeme uvažovať, že na kondenzátore môže byť najväčšie napätie U, tak maximálny prúd bude daný pomerom U/R. Z toho dostaneme vzorec pre okamžitý prúd i
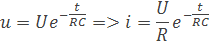
Časová konštanta má rozmer sekundy, dá sa odvodiť z rovnice τ=RC. Môžeme si to odvodiť z rozmerovej rovnice, napätie Volt V, Prúd Amper A, náboj Coulomb C a čas s.
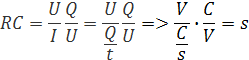
Pri nabíjaní napätie uC stúpa. Z nabíjacieho napätia U sa musí odratávať napätie Ue-t/τ. Z toho vychádza vzorec
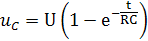
V odvodení je použitý integrál, kde jeho výsledok je prirodzený logaritmus ln. Integrovaním derivácie dostaneme pôvodnú funkciu. Keď by sme integrovali funciu x–1 podľa mocninovej integrácie dostali by sme výsledok
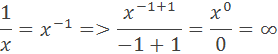
tzn. výsledok bude stále nekonečno. V blogu Načo sú nám derivácie som odvodiť deriváciu prirodzeného logaritmu (ln x)’=1/x. Z toho nám vychádza integrál
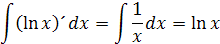
Pri zapínaní a vypínaní prúdu na indukčnosti tiež nastávajú prechodové javy. Opačný pomer prúdov na čase ako pri kapacite je na indukčnosti. Indukčnosť je určuje pomer magnetického toku na prúde ktorý ho vytvoril na určitej časti dráhy prúdu napr. vedenie, alebo cievka. Dole je nakreslený sériový obvod RL. R je činný odpor, L je indukčnosť, zdroj jednosmerného napätia U a prepínač v čase t=0. Indukčnosť závisí od parametrov cievky alebo vodiča, je konštantná. Pri pripojení jednosmerného napätia do obvodu s indukčnosťou nastane veľká zmena prúdu. Táto zmena naindukuje do vodičov prúdu opačné premenlivé napätie. To napätie má opačnú hodnotu ako napätie zdroja, je to tzv. indukované napätie ui. Indukované napätie je najvyššie hneď na začiatku.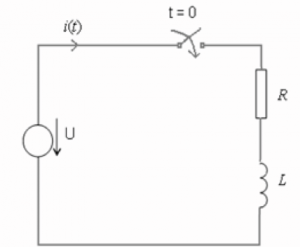
Indukčnosť môžeme odvodiť z indukovaného napätia ui, podľa vzorca.
Napätie na odpore uR je odvodené od okamžitého prúdu i. Napätie na cievke je indukované napätie ui. Indukované napätie vznikne iba vtedy keď sa zmení prúd v obvode napr. vypnutím vypínača. Indukované napätie má opačné znamienko ako napájacie napätie U. Z toho si môžeme odvodiť súčet napätí podľa vzorca
Keď vydelíme napätia odporom, dostaneme prúd.
Maximálny prúd je I=U/R. Prúd ktorý je vytvorený indukčným napätím má opačné má opačný smer pretože indukčné napätie pôsobí opačne.
Pomer L/R je podobne ako pri kapacite časová konštanta τ. Rozmer časovej konštanty pre indukčnosť si môžeme odvodiť podľa rozmeru indukčnosti. Vzorec je
Podľa vzorcov pri kapacite si môžeme odvodiť okamžité hodnoty v RL obvode, pretože keď máme časovú konštantu môžeme ju vpísať do exponentu (e-τ/t) podobne ako v RC obvode.
Odvodením podľa člena (e-τ/t) dostaneme vzorec pre okamžitý prúd
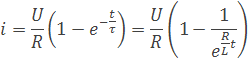
Maximálny prúd je I=U/R sa ustáli po určitom čase, teoreticky by to bolo v nekonečne ale prakticky je to v dobe keď τ/t=1. Pri vypínaní tiež dochádza k veľkej zmene prúdu. Indukované napätie má zápornú hodnotu a môže byť veľmi vysoké, pretože keď je t veľmi malé tak súčiniteľ (e-τ/t) je vysoký. Preto indukčné obvody s jednosmerným zdrojom majú veľké problémy pri zapínaní a vypínaní. vzorec pre indukčné napätie je
Na príkladoch z fyziky sa dá najlepšie vysvetliť vyššia matematika. V ďalších blogoch z fyzky odvodím ďalšie postupy s integrálmi a deriváciami.
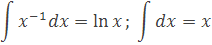
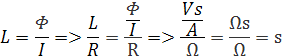
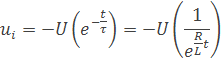




















Celá debata | RSS tejto debaty