aldebaran.pravda.sme

Pri odvodení rovnomerného zrýchlenia Newton prišiel na zaujímavý matematický spôsob počítania okamžitých hodnôt. Že pri voľnom páde je nárast rýchlosti na čase rovnomerne bolo známe. Vždy za rovnakú zmenu rýchlosti na zmene času prírastok rýchlosti bol rovnaký.

Pre konštantnú rýchlosť v_k platí, že dráha ktorú pešiel bod narásta rovnomerne. Keby sme

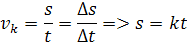
keby sme zostrojili graf tejto rýchlosti, kde na osi x je čast t ana osi y je vzdialenosť s tak spojnica bodov je priamka. Z geometrie vieme, že tangens uhla priamky je rýchlosť.

Pri priemerná rýchlosť v_p

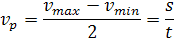
rozdiel maximálnej rýchlosti v_max a minimálnej rýchlosti v_min

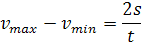
rovnomerné,konštantné zrýchlenie a_k

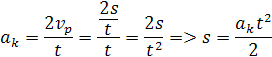
okamžitá rýchlosť pri konštantnom zrýchlení v danom čase v_kz

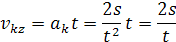
s je vzdialenosť ktorú prešlo teleso pri rovnomernom. 2s je nárast vzdialenosti pre okamžitú rýchlosť pri rovnomernom zrýchlení

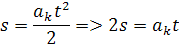
Priblíženie sa k výsledku môžeme dostať pomerom dráhy a času. dole je vzorec vzťah medzi dráhou a časom je s=t² máme vzdialenosť 16 a čas 4 tzn. okamžitá rýchlosť má hodnotu 8. čím bude zmena menšia tým výsledok bude presnejší

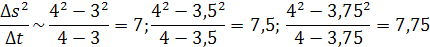
Tu sa už dostávame k derivácii

Derivácia z hľadiska geometrie predstavuje nárast funkcie v danom bode. Dole graf podľa čoho sa určuje derivácia

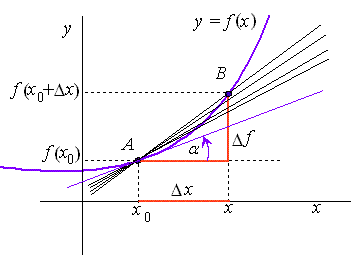
Zmeny na osiach x a sú uvedené na vzorci podľa obrázku

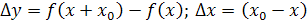
Vidíme, že čím je zmena menšia tým viac sa približuje uhol α k uhlu dotyčnice. Derivácia sa značí čiarkou a odvodzuje sa z limity podľa vzorca

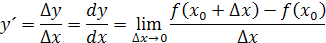
Pre y=x² dostaneme rovnicu

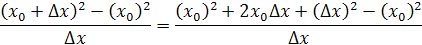
Vynásobením a vykrátením a vložením za Δx=0 dostaneme výsledok

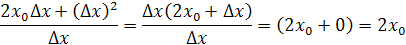
Z toho nám vyplýva vzorec pre deriváciu mocniny

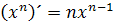
Z grafu vidíme, že y/x je tanges uhla dotyčnice, to znamená, že tangens uhla dotyčnice pri funkcii závislosti vzdialenosti na čase je rýchlosť. Deriváciou vo fyzike zisťujeme okamžitú hodnotu výslednej funkcie pri zmene základných hodnôt. Všeobecný vzorec pre deriváciu je podľa obrázka, keď zameníme za Δx h dostaneme vzorec ktorý platí pre každú jednú deriváciu.

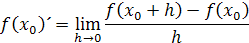
Písal som o Eulerovom čísle e je to základ prirodzených logaritmov a vyznačuje sa tým, exponenciálna hodnota tohto čísla je rovnaká. odvodím to podľa vzorca

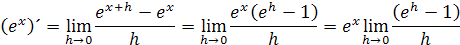
Vložením za h=0 dostávame výslednú deriváciu (e^x)´=e^x podľa vzorca

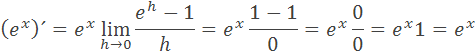
Inverzná funkcia e^x je prirodzený logaritmus ln x. Odvodenie derivácie (ln x)´ je podľa vzorca

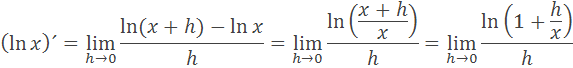
člen h/x si upravíme na člen n a podľa toho upravíme zlomok vo vzorci

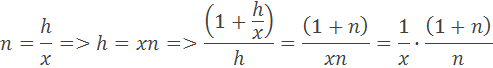
Limitu upravíme pre n sa blíži k nule a dostávame výsledné odvodenia derivácie prirodzeného logaritmu (ln x)´=1/x podľa vzorca

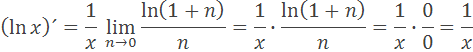
Štvrtá dôležitá derivácia je derivácia sínusu. Derivácia sínusu predstavuje tangens dotyčnice na sínusovke, funkcie sínus. Vzorec sa upraví podľa súčtu sínusov

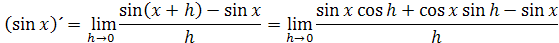
úpravou dostávame vzorec

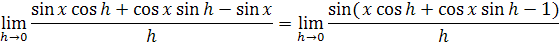
limita sa dá roztrhnúť a členy prispôsobiť aby pasovali násobkom

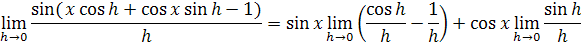
vložením za h=0 dostaneme vzorec

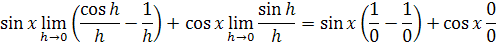
vyčíslením dostaneme hodnotu (sin x)´=cos x

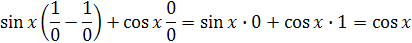
Predstavme si sínusovku v osiach x y ako dve polkružnice s polomerom 1. Dotyčnica musí mať v priesečníku os.uhol 45° voči osi x. pretože rovnomerne kopíruje povrch sínusovky. Keď budeme dotyčnicu otáčať na vrchol krivky tak jej uhol bude 0°. Hodnoty tangensov budú zodpovedať funkcie cos x. Kosínus 0° je 1 znamená to, že v bode x=1 bude uhol tangens 0. Otáčaním dotyčnice budu uhly na strane +x záporné, pretože dotyčnica sa otáča opačným smerom. Na x=1 bude uhol voči osi x -45° tzn. že tangens je –1. Hodnoty tangensu kopírujú sínus so zápornou hodnotou. Z toho vychádza (cos x)´=-sin x. Z týchto derivácii môžeme odvodiť ostatné derivácie. Deriváciu využívame na to aby sme odvodili nejaké javy, napr. výpočet rýchlosti svetla je odvodený v základe deriváciou resp. prišlo sa na to použitím derivácie.