Minule som písal čo sú to vlastne derivácie, Spomenul som v tejto súvislosti aj integrály ako opak derivácie. Integrovaním derivovanej funkcie dostaneme pôvodnú funkciu. Integrál sa označuje pretiahnutým eskom, d je diferenciál, ten nám udáva ktorú hodnotu budeme integrovať. Niekedy má nezanedbateľný význam, napíšem niečo o tom v inom blogu z fyziky. Základné vzorce pre integrály sú tieto
Prvých šesť integrálov sú tzv. neurčité integrály, posledný je určitý integrál. Pre pochopenie integrálov aj derivácii uvediem tri jednoduché príklady. Výpočet dĺžky, odvodenie povrchu plochy a objemu gule.
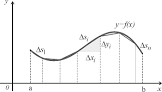
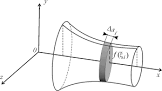
Integrálom najčastejšie počítame dĺžky krivky s. Pre názornosť dĺžku krivky si prisôsobíme tak, že ju nasekáme na malé kúsky Δsi
Vzchádzame s toho, že krivka má určitú funkciu. Dĺžku Δsi si vypočítame z Pytagorovej vety, podľa vzorca
i je ita Δsi, i=1, znamená, že sčítame všetky Δsi pretože sú rovnaké. Sčítame všetky Δsi podľa vzorca
i=1 znamená že všetky časti na osi x sú rovnaké. Čím je n väčšie tým je výsledok presnejší. Toto si môžeme prepísať do diferenciálnej formy.
z toho dostávame výsledok pre ds
na pravej strane rovnice si môžeme upraviť na
z toho dostávame výsledný integrál
Výpočet integrálu pod mocninou je dosť zložitý a niektorý sa ani nedá vypočítať. Tento pre taký integrál musíme urobiť substitúciu u a počítať podľa vzorca
Na ukážku vypočítam jednoduchý príklad hodnoty funkcie y=x3/2
Počítame vzdialenosť a=x0, b=x1. Z toho môžeme napísať integrál
substitujeme podľa vzorcov
z toho dostaneme integrál
po dosadení hodnôt dostaneme výsledok tzv. primitívneho integrálu
po úprave dostaneme
výslednú dĺžku vypočítame tak, že vložíme za x hodnoty a odpočítame ich podľa vzorca
pre x =1 je vzorec
pre x =0 je vzorec
Vynásobením 4√4=8 dostaneme vzorec
Po vykrateni sme konečný vzorec
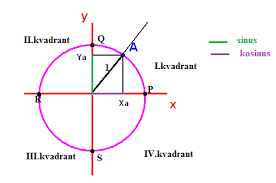
Niektoré krivky sa môžu vyjadriť pomocou parametrami a uhlom t a nejakou konštantou k. Parametre môžu byť
z toho diferenciál ds má vzorec
Parametrické rovnice pre oblúk na kružnici sú úplne jednoduché, ale keď konštanty pre sínus a kosínus nie sú rovnaké vtedy je integrál zložitý a nedá sa počítať podľa obyčajných vzorcov. Taký príklad je výpočet dĺžky elipsy.
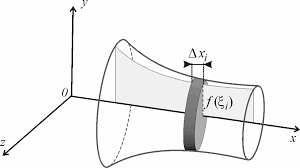
Dole sú zakreslené rotačné telesá na ktorom zakreslený jeho rez. Teleso je súmerné tzn. že pozdĺžny rez telesa udáva funkciu krivky na povrchu telesa. Narezaním rotačného telesa na malé plátky o rovnakej šírke Δx bude mať každý plátok na povrchu dĺžku Δsi. Vynásobením Δsi funkciou krivky povrchu telesa f(x) a 2π dostaneme plochu plátku ΔSi. Sčítaním jednotlivý plošiek ΔSi na vzdialenosti osi x dostaneme približnú plochu rotačného telesa. Pre presný výpočet potrebujeme integrovať jednotlivé plôšky.
Vynásobením elementárnych plošiek na polomeroch f(x)dsi ·2π dostaneme plochu elementarného plátku dSi. integráciou dostaneme plochu rotačného telesa ktoré má určitú dĺžku. Integrujeme podľa vzorca
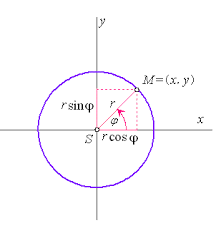
Podľa toho integrálu si môžeme odvodiť plochu gule. Predstavíme si ju ako rotujúcu polkružnicu. Polkružnia má rozpätie uhlov 0 až π. Rovnica kružnice sa dá určiť z obrázkov dole
diferenciál má vzorec
keď to vložíme do vzorca dostaneme integrál
úpravou sme získali vzorec
počítame ako určitý integrál podľa vzoru, kde
z toho dostávame výsledok
vložením dostaneme hodnotu 4πr2
Tak sme sa dopracovali k vzorcu pre povrch gule Sg =4πr2
podľa spodného obrázku môžeme odvodiť výpočet objemu rotačného telesa
Teleso si rozrežeme na malé válčeky s hrúbkou Δxi. Polomer na válčeku je rΔxi. Z toho vychádza vzorec pre ΔVi
Z toho si môžeme odvodiť diferenciál dVi
Z toho môžeme odvodiť integrál
Pretože počet válčekov je dvojnásobný pred integrálom bude 2π. Vložením hodnôt do integrálu dostaneme vzorec
Keď za x dosadíme r dostaneme vzorec
Vynásobením 2π dostaváme výsledný vzorec pre objem gule Vg =4/3πr3
Pochopiť integrály a derivácie sa dá čiastočne na jednoduchých príkladoch. Ešte napíšem niektoré príklady z fyziky kde použijem integrály a derivácie, preto som napísal tieto blogy.
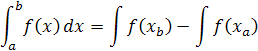
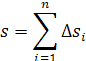
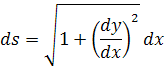
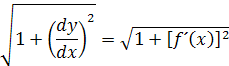
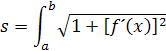
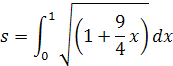
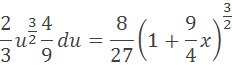
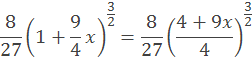
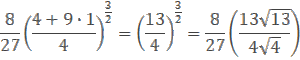
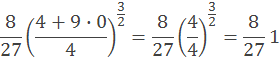
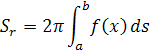
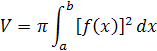
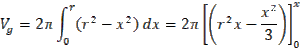
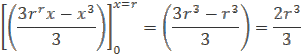




















Celá debata | RSS tejto debaty