Planckova konštanta je odvodená z merania spektra žiarenia, ktoré vyžaruje teleso teplom. Nemecký fyzik Wilhelm Wien meral intenzitu vlnových dĺžok v slnečnom spektre a zistil zaujímavú vlastnosť slnečného žiarenia. V celom spektre vlnových dĺžok mala jedná vlnová dĺžka najväčšiu intenzitu. Dole je graf ktorý zobrazuje vzťah vlnovej dĺžky slnečného žiarenia k jej intenzite.
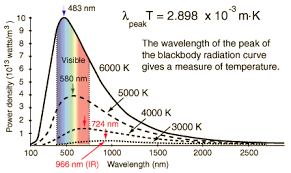
Na tomto základe začal robiť merania intenzity žiarenia na telesách, ktoré majú rôznu teplotu. Hodnoty prepočítaval na idealizované úplne čierne teleso. Úplne čierne teleso pohlcuje všetky vlnové dĺžky, ale zároveň vyžaruje všetky vlnové dĺžky pre danú teplotu. Žiarenie Slnka dosť dobre zodpovedá žiareniu úplne čierneho telesa, ostatné materiály majú určitú emisivitu, zníženie žiarenia oproti úplne čiernemu telesu. Zistil, že telesá vyžarujú celé spektrum vlnových dĺžok pri danej teplote, ale iba jedna vlnová dĺžka pre danú teplotu telesa má najvyššiu intenzitu, označil ju λmax . Pre vlnovú dĺžku λ môžeme vypočítať frekvenciu ν z rýchlosti svetla c, podľa vzorca ν=c/λ. Zaujímavé bolo zistenie, že násobok vlnovej dĺžky λmax s termodynamickou teplotou T mal vždy konštantnú hodnotu. Túto hodnotu nazvali po ňom „Wienova koštanta“ značená b s hodnotou 0.002897 7729 m⋅K. Z toho vychádza vzorec λmax=b/T. Zo vzorca vyplýva, že so zvyšujúcou teplotou vlnová dĺžka λmax sa skracuje proporcionálne. Dole je graf závislosti vlnových dĺžok na teplotách.
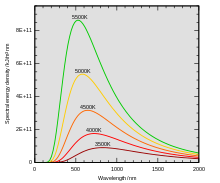
Wen potreboval očíslovať aj ypsylonovú os. Predpokladal podľa tepelnej energie molekuy, že aj energia vlny bude násobok konštanty frekvenciou. Priblížim to odvodenie konštanty, trochu polopatisticky. Na vodorovnej osi sú vlnové dĺžky λ a na zvislej je hustota žiarenia vĺn. na grafe sú znázornené krivky vyžarovania pre dané teploty. Intenzity vlnových dĺžok v spektre najprv prudšie stúpajú až po vlnovú dĺžku λmax, potom exponenciálne klesajú. Z tejto rovnice si môžeme odvodiť teplotu T pre λmax. Teplotu Tλmaxktorá zodpovedá vlnovej dĺžke
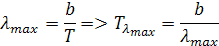
Teplotu Tλmax si môžeme vyjadriť aj pomocou frekvencie νλmax, ktorá prislúcha vlnovej dĺžke λmax. Odvodenie teploty Tνλmax pomocou frekvencie νλmax je podľa vzorca
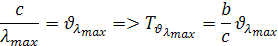
Keď vynásobíme vzorec Boltzmanovou konštantou kB dostaneme tepelnú energiu molekuly ideálneho plynu. Keď teplotu Tνλma odvodíme pomocou frekvencie νλmax dostaneme vzorec
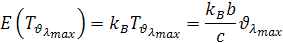
Maxwell odvodil vzťah medzi tepelnou energiou molekuly v plyne ETm a jej kinetickou energiou EKm. Pomer medzi medzi energiami má vzorec
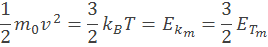
Molekula ktorá má určitú tepelnú energiu vyžaruje žiarenie o určitej energii. Energia jednej vyžarovanej vlny je generovaná kinetickou energiou jednej molekuly, preto je tiež priamoúmerná tepelnej energii tzn. je o nejaký násobok rozdielna. Z toho môžeme odvodiť pomer tepelnej energie ET(νλmax) k vyžarovanej energie Eν(νλmax)
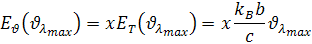
Zlomok kBb/c sú konštánty a x je tzv. číselný faktor má tiež konštantnú hodnotu. Všetky tieto konštanty sú nemenné preto si môžeme odvodiť z nich jednu konštantu h. Z vychádza výpočet pre energiu žiarenia Eν keď poznáme frekvenciu ν a môžeme si odvodiť pre frekvenciu podľa vzorca
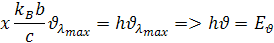
Odtiaľ dostávame vzorce pre energie žiarenia vyjadrené frekvenciou a vlnovou dĺžkou
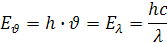
Rozmer konštanty h je Js, Joule sekunda. Pre výkon jednej vlny Pλ dostávame vzorec
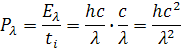
Musíme uvažovať s hustou žiarenie. Môžeme, si to predstaviť na obrázku dole, je to priestorový uhol. V strede guli je bodový žiarič. Na povrch gule o ploche r2=1m2 dopadá počet vĺn 1/λ2. Poče vĺn na polomere o dĺžke 1m=1/λ . Znamená to, že počet vĺn v priestorovým uhle je taký istý ako v kocke o dĺžke hrany 1m podľa vzorca 1/λ2 ⋅1/λ=1/λ3.
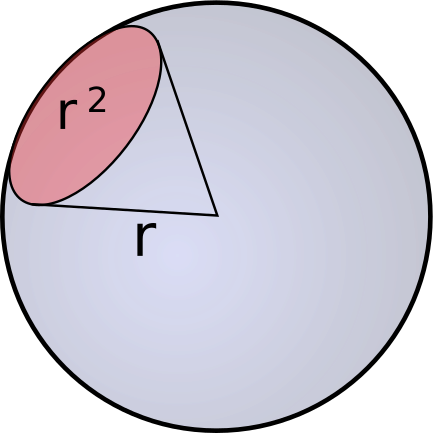
Musíme uvažovať, že vlna je trojrozmerná a nemôže mať nulový objem, preto musíme vlnu počítať v superpozícii, výkon vlny je dvojnásobný. Z toho nám vychádza vzorec pre hustotu výkonu vyžarovaných vĺn z rovnakou vlnovou dĺžkou na steradián Bλ. Jej rozmer je W/m3
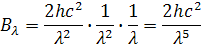
Na grafe je vidno, že pri zväčšovaní vlnových na dĺžok hustota žiarenia najprv prudko potom sa krivka prudko ohne po vlnovú dĺžku λmax. Ďalším zväčšovaním vlnovej dĺžky od λmax hustota žiarenia mierne exponenciálne klesá. Znamená to, že častice zohriateho telesa sa pohybujú chaoticky. Vyžarovaná hustota výkonu jednotlivých vĺn v spektre kopíruje kinetickú energiu jednotlivých častíc hmoty telesa. Wien si pomohol s Maxwell Boltzmanovým distribučným zákonom. Tento zákon určoval pravdepodobnosť koľko častíc plynu sa bude pohybovať určitou rýchlosťou. Dá sa určiť najpravdepodobnejšia rýchlosť a z nej možno odvodiť graf. Tento graf bol veľmi podobný z grafom vlnových dĺžok. Boltzmann vypracoval zákon pre počet častíc ideálneho plynu ktorý sa nachádza v reze stĺpca v určitej výške. Predstavme si rovný valec, ktorý je kolmý na zem a napustený ideálnym plynom. Dole je N0 častíc. Čím bude plyn teplejší tým bude väčšia hustota častíc. Rozdiel medzi množstvom častíc v priereze N0 a N bude menší. Tepelná energia častíc bude vyššia. Čím bude plyn ťažší a prierez stĺpca N bude vzdialenejší od prierezu N0 tým bude väčšia zmena gravitačnej energie. Znamená to, že násobok N0 deriváciou pomeru zmene gravitačnej energie molekuly k tepelnej energie molekuly plynu nám udáva počet častíc N. Keď označíme hmotnosť molekuly m0, g gravitačné zrýchlenie a hG výšku od zeme dostaneme zmenu gravitačnej energie ΔEG. Tepelná energia je násobok Boltzmanovej konštanty kB termodynamickou teplotou T. Z toho vychádza vzorec

V plyne ktorý má určitú teplotu nepohybujú sa všetky molekuly rovnakou rýchlosťou. Výpočtom z tepelnej energie sa dá určiť najväčší počet molekúl, ktoré sa budú pohybovať rovnakou rýchlosťou. Pri zvyšovaní rýchlostí počet molekúl pre danú rýchlosť prudšie stúpa. až po najpravdepodobnejšiu rýchlosť. Rýchlosti ktoré stúpajú od najpravdepodobnejšej rýchlosti, mierne exponenciálne klesajú. Vo vzorci je exponenciálny násobok podobný ako v predchádzajúcom vzorci, len miesto zmeny gravitačnej energie je kinetická energia molekuly. Čím je hmotnosť molekuly väčšia tým bude objemnejšia a čím bude rýchlejšia, tým kratšie vlny bude vyžarovať. Znamená to, že väčšia kinetická energia molekuly vyžaruje svetelnú vlnu s väčšou energiou, Z toho si môžeme odvodiť exponenciálny násobok pre vlnovú dĺžku.
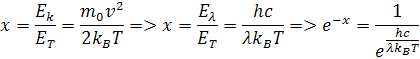
λVložením exponenciálneho násobku do hustoty jednej vlnovej dĺžky, dostávame objemovú hustotu svetelných vĺn v spektre zohriateho telesa pre danú teplotu B(λ; T)
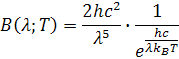
V konštante h je neznáma hodnota číselného faktora x. Vlnová dĺžka je λmax je na vrchole krivky tzn. dotyčnica je rovnobežná s osou x a tangens dotyčnice je 0. Keď B(λ; T) derivujeme podľa vlnovej dĺžky λ a výsledok derivácie bude 0 , z tejto derivácie si môžeme si odvodiť vzorec pre výpočet číselného faktora. Vzorec pre derivovanie má tvar
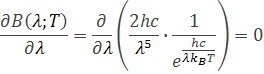
Derivujeme podľa vzorca
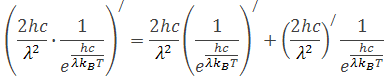
výpočet derivácii pre exponenciálny násobok sa počíta podľa tzv. reťazenia
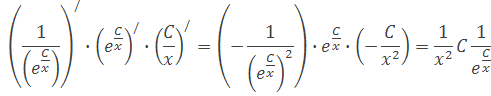
keď za x vložíme λ a za konštantu C vložíme hc/kBT dostaneme vzorec
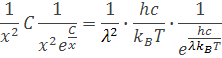
prvá derivácia sa počíta ako mocninová, kde miesto konštanty C1 vložíme hc z toho dostanem vzorec
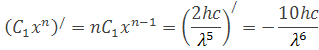
Vložením jednotlivých derivácii do rovnice pre násobenie derivácii, si z nej môžeme odvodiť vzorec pre hodnotu číselného faktora x=hc/(λmaxkBT) podľa vzorca
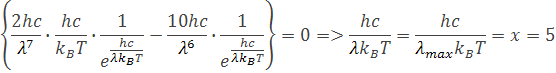
Z tejto rovnice vychádza číselný faktor x=5. Z toho si môžeme odvodiť rovnicu pre výpočet konštanty h
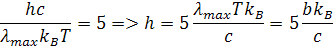
Keď som vložil hodnoty b, kB a c do excelu a vyšla mi približná hodnota hodnota konštanty h vo vzorci
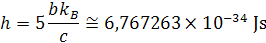
Tento vzťah odvodil Wien v roku 1896. Výpočet celkom presné vychádzal pri meraní kratších vlnových dĺžkach, ale pri dlhších bol výpočet nepresný. Tento vzťah nebol celkom presný. Pretože konštanta h sa odvodí z výsledného vzorca tak jej hodnota tiež nemohla byť celkom presná. V roku 1900 odvodili presný vzťah Nemecký fyzik Max Planck. Jeho výpočty presne kopírovali meranie, preto mohol mohol presne určiť hodnotu konštanty h, ktorú po ňom pomenovali. Wien odvodil výpočet pre energiu vyžarovanej vlny, čo bolo veľmi dôležité.




















Celá debata | RSS tejto debaty