Pokračujem v doplnení článku o vyžarovaní svetla teplom. Wien správne odhadol, že energia svetelnej vlny bude mať určitú pomernú konštantu. Ale jeho rovnica pri väčších vlnových dĺžkach nevyhovovala meraným hodnotáam. Popísať svetelné spektrum sa pokúsili anglickí fyzici lord Rayleigh a sir James Jeans. Odvodení ich zákona je na internete niekoľko. Ale najjednoduchšie odvodenie pre pochopenie ich zákona, je to ktoré je matematický najťažšie. Je to odvodenie z Maxwellových vlnových rovníc, pretože už sa predpokladalo, že svetlo je elektromagnetické vlnenie. Označenie spektrálnej hustoty žiarenia je tiež rôzne. Objemová hustota sa označuje niekedy H, Me a u.
Vychádzali z úvahy: v zohriatom telese sa elektromagnetická vlna sa bude vytvárať vo fiktívnych dutinách. Dutina má určitý objem kde je stojatá elektromagnetická vlna. Predstavme si kocku s veľkosťou strany λ a v nej je vlna ktorá je guľa s polomerom (λ/2)=L. Vychádzali z toho, že stojatá vlna sa bude odrážať od stien v kocke, ktorá má objem λ3. V kocke je guľa s polomerom L. Objem gule je Vg=(4∙π∙L3)/3. Pomer objemov Vg/λ3 označili ako mod N. Vzorec je ![]() Je to určitá voľnosť elektromagnetickej vlny. Tento vzorec popisuje iba statickú vlnu. Uvažujme, že keď je vlna guľa tak sa bude stláčať v rytme frekvencie. V kocke bude určitá hustota vlny. Hustotu vlny môžeme prirovnť k rýchlosti stláčania vlny. Keďže uvažujeme vlnovú dĺžku ako trojrozmernú guľu ktorá sa stláča, tak svoju dĺžku mení. V kocke musíme uvažovať 2 vlny v protifáze, pretože jedna by v strede vlnovky mala nulový objem. Jedna guľu rozťahujeme a druhá sa stláča v rovnakom čase a v jednom priestore. Deriváciou modu N na vlnovej dĺžke λ dostaneme hustotu elektromagnetickej vlny. Môžeme to prirovnať k objemu dN na vlnovej dĺžky dλ. deriváciou dostávame vzorec
Je to určitá voľnosť elektromagnetickej vlny. Tento vzorec popisuje iba statickú vlnu. Uvažujme, že keď je vlna guľa tak sa bude stláčať v rytme frekvencie. V kocke bude určitá hustota vlny. Hustotu vlny môžeme prirovnť k rýchlosti stláčania vlny. Keďže uvažujeme vlnovú dĺžku ako trojrozmernú guľu ktorá sa stláča, tak svoju dĺžku mení. V kocke musíme uvažovať 2 vlny v protifáze, pretože jedna by v strede vlnovky mala nulový objem. Jedna guľu rozťahujeme a druhá sa stláča v rovnakom čase a v jednom priestore. Deriváciou modu N na vlnovej dĺžke λ dostaneme hustotu elektromagnetickej vlny. Môžeme to prirovnať k objemu dN na vlnovej dĺžky dλ. deriváciou dostávame vzorec![]() Tento vzorec ale udáva iba hustotu v kocke. Z toho si môžeme odvodiť hustotu vvĺn v jednotkovom objeme u podľa vzorca
Tento vzorec ale udáva iba hustotu v kocke. Z toho si môžeme odvodiť hustotu vvĺn v jednotkovom objeme u podľa vzorca ![]() Keď vynásobíme člen
Keď vynásobíme člen
8π/λ4 Boltzmanovou konštantou kB a termodynamickouj teplotou T dostaneme objemovú hustotu energie elektromagnetickej vlny Hλ. Násobok kB·T nám udáva tepelnú energiu jednej molekuly ET. Z toho vychádza vzorec
Môžeme si to vyjadriť aj s frekvenciou.
derivujeme mod Nν na frekvencii ν podľa vzorca
Z toho dostávame objemovú hustotu frekvencie uν
Podobne vynásobením ET∙uν dostávame hustotu energie elektromagnetickej vlny vyjadrenú frekvenciou Hν
Číselné hodnoty nie sú rovnaké, pretože v jednej uvažuje sa vlnová dĺžka a v druhej frekvencia. Grafy nie sú rovnaké, pretože energia stúpa so zvýšujúcou frekvenciou tzn. so zväčšujúcou vlnovou dĺžkou energia klesá.
Plochu steradiánu dostaneme tak, že vydelíme obsah gule 4π. Spektrálna hustota žiarenia B predstavuje počet vĺn v priestorovom uhle. Počítame počet vĺn na plochu steradiánu a na polomer.
Vynásobením rovníc pre hustoty elektromagnetických vĺn a frekvencie členom c/4π dostaneme podobne ako vo Wienovom vzorci hustotu výkonu žiarenia danej vlnovej dĺžky na steradián podľa
a pre frekvenciu dostaneme hustotu energie elektromagnetických vĺn na ploche steradiánu. Prepočet je podľa vzorcov
Prevod medzi hustotou vlnovej dĺžky v steradiáne a hustotou energie frekvencie vĺn na ploche steradiánu je podľa vzorca
Podľa týchto rovníc si môžeme určiť rozmerové rovnice. Pre hustotu výkonu vlnových dĺžok je rozmerova rovnica
Rozmerová rovnica pre hustotu energie frekvencie elektromagnetických vĺn na ploche steradiánu je odvodená, podľa vzorca
Hodnoty vo vzťahoch nie sú číselne rovnaké pretože pri vlnovej dĺžke udávame výkon v objeme a pri frekvencii je udaná energia na ploche. Energiu na ploche je súčet energie všetkých vlnových dĺžok na ploche steradiánu. Rayleigh- Johnsonov vzťah intenzity danej frekvencie spektra úplne čierneho telesa na jednotku plochy bol pomerne presný iba pri menších frekvenciách. Teleso vyžaruje rôzne frekvencie pri danej teplote ale intenzita od určitej frekvencie začína klesať. Podľa Rayleigh – Jeansovho vzťahu intenzita stúpa s frekvenciou stále. Tieto dilemy vedci pomenovali ultrafialová a infračervená katastrofa. Vlnovú dĺžku odvodili podobne ako Wien, ale ignorovali konštantu ktorú Wien navrhol. Ich merania pre väčšie vlnové dĺžky boli pomerne presné.
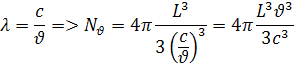






















Celá debata | RSS tejto debaty