aldebaran.pravda.sme

Wienové merania boli správne iba pri veľmi malých vlnových dĺžkach. Rayleigh a Jeans sa snažili túto anomáliu vysvetliť ale konštantu h zanedbali, čo urobili veľkú chybu. O tom vzťahu som písal v minulom blogu. Meraním pri väčších vlnových dĺžkach bol ich vzťah správny. Nemecký fyzik Max Planck porovnával výsledky meraní s vypočítanými hodnotami a vzťah upravil. Dole na grafe sú znázornené krivky výpočtov podľa meraní. Modrá Planckova krivka zodpovedá meraným hodnotám, červená je Wienova charakteristika a čierna je Raylegh-Jeansonova charakteristika. Wienova krivka je veľmi nepresná pri dlhších vlnách ale pri menších vlnách kopíruje krivku merania. Raylegh-Jeansonova krivka je presná pri dlhých vlnách ale iba vo veľmi malom úseku.

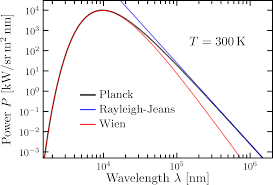
Z toho grafu vyplýva, že hodnotu vo Wienovom vzťahu

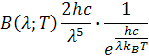
musíme zväčšiť a Rayleigh – Jeansov-vzťah

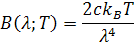
musíme zmenšiť podľa odvodeného násobku

Planck intuitívne odvodil nerovnosti z funkcie e^x, podľa vzorca

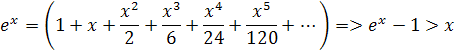
za x vložíme hodnoty podľa vzorca

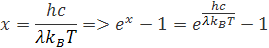
Z toho si môžeme odvodiť vzorec

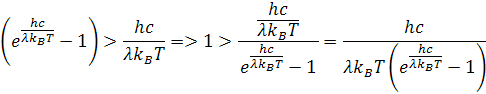
Vynasobenim Rayleigh – Jeansonov vzťahu výsledkom z vrchného vzorca, dostaneme upravený Wienov vzťah.

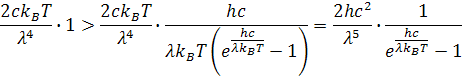
Takto sme dostali upravený Wienov vzťah pre hustotu vyžarovaných vlnových dĺžok, ktoré vyžaruje úplne čierne teleso pri danej teplote. Planckov vzťah

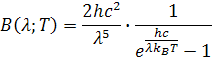
Pri veľmi krátkych vlnových dĺžkach je exponent veľký, -1 môžeme zanedbať, Pri väčších vĺnových dĺžkach je exponent malý, tu sa už vo výsledku sa prejavuje -1. Takto určený vzorec dobre kopíroval krivku výsledkov meraní. Hodnota konštanty h sa musela spresniť, pretože vzorec sa upravil. Pri odvodení postupujeme podobne ako pri Wienovom odvodení. Derivujeme Planckov vzťah podľa vlnovej dĺžky λ

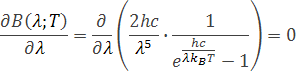
Výsledok derivácie má vzorec

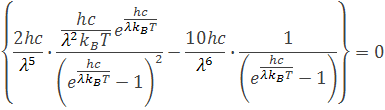
úpravou dostaneme rovnicu

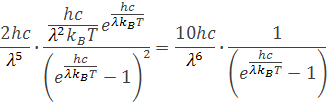
vykrátením dostaneme vzorec

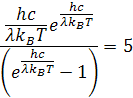
Táto rovnica nedá priamo vypočítať, Musíme exponent prepísať podľa vzorca

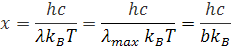
Potom dostaneme rovnicu z ktorej si môžeme vyjadriť x

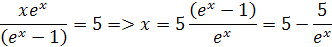
x je číselný faktor, ten sa nedá jednoducho vypočítať, pretože táto rovnica obsahuje člen xe^x. Presnejšie sa určí tzv. Lambertovou W funkciou, podľa vzoru

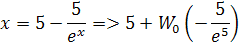
Z tejto rovnice dostaneme vzorec

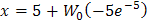
Člen W₀ sa určí numerickou metódou v Taylerovom rade podľa vzoru

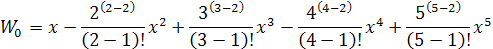
keď upravíme exponent a vypočítame fakoriály dostaneme výpočet

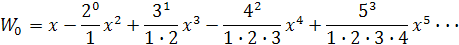
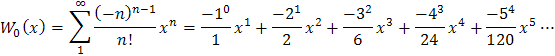
za x vložíme číslo s hodnotou (-5e^-5). Asi desiatom rade vypočítame hodnotu x s dosť veľkou presnosťou. Presnejšie vychádza W₀ = -0,0348857682557237 ktoré bolo určené

Číselný faktor má hodnotu 5-0,0348857682557237 = x =4,965 114 231 744 276 303.

konštanty b, k_B, c poznáme a číselný faktor x sme vypočítali. Vložením týchto hodnôt do rovnice, vypočítame hodnotu Planckovej konštanty h podľa vzorca

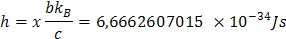
Hodnota vo vzorci sa veľmi málo odlišuje od udávanej hodnoty, pretože Planckova konštanta je meraná.