Skúsim do tejto prepolitizovanej doby napísať článok apolitický. Dokončím reakciu na článok ktorý písal Stan 021. V predchadzajúcom blogu som odvodil vzorce pre výpočet rozmerov reťazovky. V tomto blogu odvodím základnú deriváciu pre reťazovku. Začnem popisom grafu ktorý opisuje pôsobenie síl na reťazovke.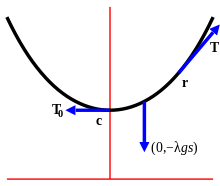 
Na grafe sú znázornené 3 sily. λgs , T0 a výsledná sila T. Sila λgs je vlastne váha reťazovky medzi bodmi c a r. λ je element reťaze, g je gravitačné zrýchlenie a s je dĺžka reťaze medzi bodmi c a r. Táto sila pôsobí kolmo dole. Sila λgs pôsobí v súbežne s osou y, znamená to, že sila λgs je úmerná hodnote Δy. Silu T0 si môžeme predstaviť ako silu ktorá ťahá stredný element reťaze do jednej strany. Sila T0 je súbežná s osou x, znamená to že je kolmá na silu λgs a je umerná hodnote Δx. Sila T0 je závislá od sily λgs, preto pri jej určení miesto dĺžky s použijeme fiktívnu dĺžku, ktorá je parametrom reťazovky a. Parameter vo výpočtoch určuje základnú výšku od najnižšej vzdialenosti reťazovky od zeme pri zadaných hodnotách s x y. Z toho si môžeme odvodiť vzorec, kde miesto zmeny Δx a Δy použijeme diferenciály dx a dy
Element dĺžky reťaze ds si môžeme odvodiť z Pytagorovej vety kde odvesny sú dx a dy a prepoona je ds podľa vzorca
vydelením rovnice dx dostaneme deriváciu
Z tohto vzorca si môžeme odvodiť diferenciál dx
Pre výpočet x musíme všetky dx spočítať, integrovať. Integrácia je v podstate násobenie derivácie. Počíta sa opačne ako derivácia. Integral má vzorec
Tento integral som odvodili v minulom blogu. Takto sme odvodili polovičnú vzdialenosť reťazovky medzi stĺpmi x. Podľa vzťahu medzi sínusom a inverzným sínusom
si môžeme vypočítať polovičnú dĺžku reťaze s
V prvej rovnici sme odvodili diferenciál dy , ten potrebujeme pre výpočet výšky stĺpca y. Rozpísaním za s dostávame rovnicu
V minulom blogu som písal, že derivácia sin u sa rovná -cos u. Pri derivovaní hyperbolických funkcii sinh a cosh môžeme požiť také isté pravidlá pretože rovnice kružnice a hyperboly sú podobné. Keďže integrál je opak derivácie dostávame integráciou dy výšku stĺpca y podľa vzorca
Vo výpočtoch sa najčastejšie stretávame kde sú udané 3 hodnoty, vtedy parameter a nepoznáme, musíme ho vypočítať a vložiť do rovnice ktorú potrebujeme vypočítať. Parameter sa nedá vypočítať obyčajnou rovnicou. Vypočítava sa z parametrickej rovnice, ktorú si ostavíme z rovníc pre hodnoty ktoré sú udané. V minulom blogu som riešil dĺžku x pri výške stĺpca yzh a najnižšej výške reťazovky od zeme azh. Keďže nevieme či hodnota azh sa rovná parametru, znamená to, že zadaná výška stĺpca sa nerovná y. Z toho si môžeme odvodiť predlženie stĺpca p.
Píšem hodnoty ktoré sú zadané ako zh aby sa vedelo ako sa má zostaviť algoritmus. V minulom blogu som počítal dĺžku x. Parameter a som odvodil z parametrickej rovnice, ktorá je odvodená z výpočtu výšky stĺpca y a výpočtu vzdialenosti x podľa vzorca do
tejto rovnice vkladáme za a hodnoty až sa bude hodnota yzh rovnať zadanej hodnote. Odvodený parameter z algoritmu vložíme do rovnice pre výpočet dĺžky x.
Keď nepoznáme s a poznáme yzh, xzh a azh tak algoritmus sa zjednoduší
odvodený parameter vložíme do vzorca pre s
Keď poznáme hodnoty szh, xzh a azh môžeme vypočítať výšku stĺpca s predĺžením y+p. Parameter odvodíme zo vzorca pre dĺžku reťaze szh alebo vzdialenosti xzh
y+p vypočítame podľa vzorca
Na výpočet parametrických rovníc existuje veľa spôsobov. Dnes ale najlepšie je urobiť program v počítači podľa algoritmov a parameter je určený v zlomku sekundy.
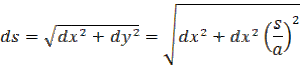
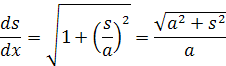
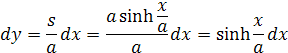
Celá debata | RSS tejto debaty