Do rozbúrených politických blogoch napíšem apolitický blog ktorý nie je zaujímavý ale možno si ho niekto aj prečíta.
Zájdem trochu do minulosti. Taliansky matematik hvezdár a učenec galileo v 17. Storočí odvodil jednoduché rovnice pre časy, vzdialenosti a rovnomerné rýchlosti. V krátkosti zjednodušene opíšem tie vzorce. Pohybujem sa rovnomernou rýchlosťou v na vzdialenosti x. Za určitý čas t prejdem vzdialenosť v·t. Predo mnou bude zvyšok vzdialenosti x´. prvá rovnica je výpočet vzdialenosti x´a druhá je súčet ktorá nám udáva vzdialenosť x
Vydelením týchto rovníc časom t získame rovnice pre súčet rýchlostí. x/t=ω je súčet a x´/t=u je rozdiel rýchlosti. Rovnice sú jednoduché
Problém pri týchto transformáciách vzdialenosti času na rýchlosť nepočítal s maximálnou rýchlosťou svetla c. O tom sa začalo špekulovať až po odvodení rýchlosti svetla. Nemecký fyzik Hendrik Lorentz spolupracoval aj s Einstejnom odvodil vzťah pre pôsobenia síl medzi dvoma letiacimi elektrickými nábojmi vo vákuu. Elektrické náboje pohybom vytvárajú magnetické pole. Medzi dvoma nábojmi bude preto pôsobiť elektrická aj magnetická sila.
Elektrická sila letiacich nábojov q1 a q má vzorec
E je elektrická intenzita elektrického náboja ktorá pôsobí na druhý náboj r je vzdialenosť nábojov a ε0 je elektrická vodivosť prostredia permitivita. Znak × znamená, že násobiť rýchlosti sa musia tak ako keby leteli vedľa seba. Prepočítava sa ich vzájomná rýchlosť z ohľadom na smer rýchlosti. Šípka nad písmenami hodnôt znamená že majú určitý smer.
Magnetická sila Fm ktorá pôsobí na letiaci elektrický náboj q v magnetickom poly má vzťah
Magnetická indukcia letiaceho náboja vo vákuu je
Magnetická sila medzi dvoma letiacimi nábojmi vo vákuu kde ich rýchlosti sú v1 a v2, môžeme odvodiť nasledovne. Náboj q má rýchlosť v1 a druhý náboj má intenzitu E voči náboju q a pohybuje sa rýchlosťou v2. Z toho môžeme odvodiť vzťah
Pre dva letiace náboje vedľa seba budú ich magnetické sily pôsobiť proti elektrickým silám Celkový vzťah pre dva náboje ktoré letia vedľa seba vo vákuu je rozdiel obidvoch síl elektrickej a magnetickej sily
Magnetické sily letiacich nábojov pôsobia opačne ako elektrické sily. Keď budú obidva náboje mať rovnakú polaritu tak sa budú odpudzovať ale magnetické sily ich budú priťahovať. Pri nerovnakej polarite nábojov sily pôsobia opačne. Tento vzťah si môžeme si odvodiť vzťah podľa rýchlosti svetla c
z toho sa dá odvodiť vzorec pre silu ktorá pôsobí medzi dvoma letiacimi nábojmi vo vákuu
Z toho vzorca vyplýva, že aby išli dva elektrostatické náboje vedľa seba rovnomerne, tak musia mať rýchlosťou c, pretože ich magnetické a elektrické sily sú rovnaké. Ale pri takom blesku sa iony pohybujú rýchlosťou okolo 200 km/s a to už nie je zanedbateľná rýchlosť. Keď uvážime, že v kozme môžu lietať častice voči sebe obyčajným súčtom väčším ako rýchlosť svetla vo vákuu tak potom by výpočty síce sedeli sedeli ale z hľadiska pôsobenia elektrických a magnetických polí nie. Podľa toho sa musel súčet rýchlostí prispôsobiť tak aby súčet rýchlostí ω= v1+v2 bol vždy menší ako c, ale pri nižších rýchlostiach by výsledok bol presný.
Aby sedeli transformácie museli sa upraviť transformáciu x´ podľa rýchlosti svetla a pridať aj transformáciu času t´. Aby výpočet bol správny bolo potrebné zohľadniť určitý faktor gama γ, ktorý zvyšoval rozdiely hodnôt v závislosti od rýchlosti sústavy voči rýchlosti svetla.
Vzťahy pri Lorentzovej transformácii pre vzdialenosti x’=ct‘ a x=ct sú odvodené zo vzorcov

Vzťahy pri Lorentzovej transformácii pre čas t´=vx’/c2 a t=cx/c2 sú odvodené zo vzorcov

Faktor gama odvodime z násobku x’x podľa vzorca

Roznasobenim a vykrátenim dostaneme rovnicu

Vydelenim c2 a úpravou dostaneme vzorec

Z tohto vzorca si môžeme odvodiť faktor gama γ

Vložením odvodenia gamafaktora γ pre vzdialenosť x´, x a čas t´, t dostaneme vzorce


Zo súčtu relativistických rýchlostí môžeme odvodiť rozdiel rýchlostí, podľa vzťahov

Pre súčet rýchlostí dostávame v odvodeni, že súčet rýchlosti nikdy neprekročí rýchlosť svetla a aj súčet c+v=c

Pre rozdiel dostaneme po odvodení dostaneme výslednú rýchlosť vždy väčšiu ako pri obyčajnom odvodení. Podobne ako pri súčte je rozdiel c-v=c

Tieto rovnice sa nedali praktický overiť, ostali len v akademickej rovine. Až neskôr Einstein transformácie odvodil pri definovaní relativistickej hmotností a dilatácii času.
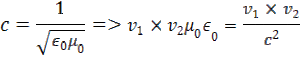




















dakujem vám za príspevok. ...
Pri citani som sa preladila do mladsej podoby, ...
Celá debata | RSS tejto debaty