Do búrlivých politických blogov zase píšem jeden nezáživný blog.
Pozeral som film o Einsteinovi a bola tam scéna, kde uvidel na stanici prechádzajúci vlak do ktorého narazil blesk. Einstein mal bohatú predstavivosť a svoje myšlienkové pochody nazýval myšlienkový experiment. Predstavil si vlak ktorý sa pohyboval rovnomernou rýchlosťou v blízkou rýchlosti svetla c a na konci vagóna udrel blesk. Vzdialenosť medzi strechou vagóna a podlahou je L. Svetlo zo strechy vagona na podlahu dopadne za čas keby vagón stál čas t0=L/c. ale keď sa bude vagon pohybovať rýchlosťou blízkou rýchlosti svetla, tak podlaha sa posunie o vzdialenosť v·t.
Dráha c·t0 je kolmá na dráhu v·t. Svetlo dopadne na podlahu ako prepona pravouhlého trojuholníka, ktorá má dĺžku c·t0. Podľa obrázku si môžeme odvodiť čas t Pytagorovej vety




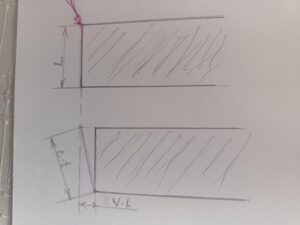
Predstavme si vagón ktorý má dĺžku L0 =t0c a pohybuje sa relativistickou rýchlosťou v. Z prednej steny vystrelí fotón oproti smeru jazdy. Na zadnú stranu dopadne skôr, pretože zadná stena sa posunie o dĺžku t0v. Keby sme sa pozerali na letiaci predmet pri relativistickej rýchlosti videli by sme ho kratší. Rozdiel vzdialenosti môžeme určiť z dvoch sústav. Na sústave S ktorá sa nepohybuje je vzdialenosť na začiatku predmetu x2 a na konci predmetu je vzdialenosť x1. Predmet sa pohybuje v sústave S´. V sústave S´ na začiatku predmetu je vzdialenosť x2´ a nakonci je vzdialenosť x1´. Pri rýchlosti 0 sa musia rovnať rozdiely (x2´ –x1´)=(x2 –x1) pretože teleso stojí a jeho dĺžka je L0. Môžeme to odvodiť zo vzorca
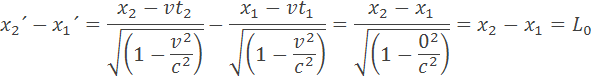
Pri pohybe sa bude dĺžka L0 skracovať. Z toho môžeme odvodiť vzorec pre vzdialenosť L ktorú uvidíme v sústave S
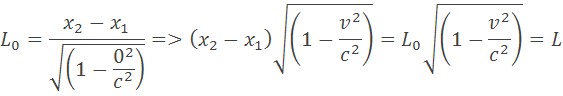
Tak Einstein dokázal aj keď iba v teoretickej rovine, že transformácie fungujú. Predlžovanie, dilatáciu času je ťažšie pochopielná, ale skracovanie dĺžok sa dá pochopiť aj z obyčajným rozdielom vzdialenosti.




















Celá debata | RSS tejto debaty