Ako som písal minule Einstein tušil, že hmota je nejaký iný stav elektromagnetických vĺn. Hmota sa fakticky skladá s elektrických nábojov a väzbových síl. Keď sa uvoľnia väzbové sily tak elektrické môžu pohybom vyžarovať energiu, preto Lorentzove rovnice by mali platiť pre každé teleso.
Ďalším jeho myšlienkovým experimentom sa zaoberal zachovaním hybnosti telies.
Hybnosť p je rýchlosť telesa v krát jeho hmotnosť m. Keď zvýšime hmotnosť telesa behom jeho pohybu tak sa zníži rýchlosť v závislosti od hmotnosti. Ale súčin ostane rovnaký. Vzorec pre hybnosť je p=m·v. Keby sme telesu o hmotnosti m v pohybe pridali alebo odobrali hmotnosť jeho rýchlosť sa upraví v závislosti na hmotnosti tak aby súčin hmotnosti a rýchlosti bol rovnaký. Môžeme si to demonštrovať pri nepružnom náraze telies. Predpokladajme, že teleso o hmotnosti m ktoré sa pohybuje narazí do stojaceho telesa o hmotnosti m0. Zanedbajme prechodový jav pri náraze. Ďalej sa už budú pohybovať obidve hmotnosti m+m0 spolu rýchlosťou zníženou o rýchlosť v. Hmotnosť sa zvýši, preto rýchlosť sa musí znížiť ale celková hybnosť ostane. Vzorec je
pre zníženú rýchlosť u môžeme odvodiť vzorec
Rozpísaním do vzorca pre hybnosť dostaneme vzorec.![]()
Rozdiel rýchlostí blížiacch sa rýchlosti svetla musíme počítať podľa relativistických vzťahov pre skladanie rýchlostí
Keby sme uvažovali že telesá m+m0 letia pri rýchlosťou ω´ ktorá sa blíži k rýchlosti c tak musíme vložiť za u do relativistickej rovnice. Vložením rýchlosti do vzorca pre hybnosť dostávame vzorec
v vykrátime a vynásobíme člen 1-mv2/c2(m+m0) a po roznásobení dostaneme vzorec
Vynásobením rovnice členom c2(m+m0) dostaneme rovnicu
Člen c2(m·m0) v rovnici sa vykráti a dostaneme rovnicu
Vydelením rovnice c2 dostaneme rovnicu
Vydelením 1-v2/c2 a odmocnením dostaneme rovnicu
Takto jednoducho odvodil Einstein vzťah pre relativistickú hmotnosť
Relativistická hmotnosť sa prejavuje pri rýchlosti blízkej rýchlosti svetla. Pri malých rýchlostiach vystačíme s Newtonovou mechanikou. Keby teleso sa pohybovalo rýchlosťou c muselo by mať nekonečnú hmotnosť. Preto rýchlosťou svetla sa môže pohybovať iba fotón pretože má nulovú kľudovú hmotnosť m0 resp. v kľude neexistuje
Ale ako to môžeme dokázať? Gravitačné účinky sa nebudú pri relativistickej rýchlosti zvyšovať a odvážiť to nie je možné. Zase je to iba myšlienkový experiment. Ale existuje možnosť ako zmerať kinetickú energiu pri takýchto rýchlostiach. Častice atómov v elektrickom a magnetickom poli môžeme urýchliť na rýchlosť blízku rýchlosti svetla. Ich rýchlosť sa dá zmerať. A pri zrážkach sa dá zmerať ich kinetická energia. O energii na píšem nabudúce. Zatiaľ je to iba matematické cvičenie ale aby som chcel vysvetliť prečo atómová energia má takú silu musím niektoré časti vysvetliť matematicky.
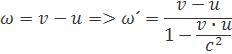
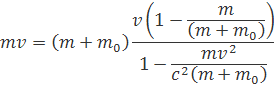
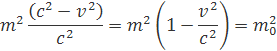
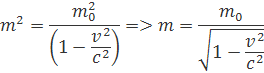
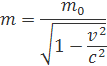




















dakujem za príspevok. je tam dosť vzorcov ale ...
Rád čítam o myšlienkových experimentoch ...
Celá debata | RSS tejto debaty