Do korovírusovej doby pokračujem v svojich neaktuálnych blogoch o hmote. Dostal som sa trochu na začiatok zaujímavého fenómenu, časticiam v priestore pre ktoré neplatí klasická mechanika. Pre tento blog je potrebná aj dosť veľká predstavivosť.
Predstavme si atóm vodíka. Ten má jadre 1 protón ktorý má kladný náboj a vo vzdialenosti re obieha okolo rýchlosťou ve elektrón. Priťahujú sa elektrostatickou silou Fqe. Aby elektron nepadol do jadra musí mať dostatočnú odstredivú silu Foe.
vynásobením dostaneme vzorec
Elektróny sa pohybujú v atómoch podľa Rhuterforda po eliptických dráhach podobne ako planéty. Ale Bohr vypočítal vlastnosti elektrónov ako keby sa otáčali v rovnomerných vrstvách. Energie elektrónov vo vrstvách musia byť kvantované, pretože každá vrstva má iný polomer a elektrón medzi nimi nemôže obiehať. Pri preskoku elektrónu z jednej vrstvy na druhú, jeho energia bude rovnajúcu sa rozdielom energie v orbitáloch elektrónu Ef =ΔEo1 -ΔEo2. Znamená to, že moment hybnosti elektrónu vodíka Lpe musí byť rovný Planckovej konštante h. Pre elektrón vo vodíku vychádza vzorec
2πr obvod kruhu čo je rovný dĺžke vlny λ.
re je polomer atómu, ve je rýchlosť elektrónu me je hmotnosť elektrónu qe je elektrický náboj elektrónu a protónu a h je Planckova konštanta. Poznáme hodnotu me a ostané sú konštanty. Z týchto rovníc si môžeme vypočítať polomer atómu vodíka a rýchlosť elektrónu v orbitále. pre výpočet polomeru sa počíta z rovnosti síl, podľa vzorcov
vynásobením dostaneme rovnicu
úpravou rovnice na ľavej strane dostaneme vzorec
vydelením me a πdostaneme vzorec s ktorého si môžeme odvodiť polomer atómu vodíka re
rovnice pre silu upravíme na tvar
podľa vyjadrenia základného momentu hybnosti elektrónu dostaneme v vzorec
vydelením h dostaneme vzorec pre rýchlosť elektrónu v orbitále vodíka
Elektróny sa pohybujú v orbitaloch ktoré môžu mať 7 energetických hladín n a atómy majú Z protónov. Vzorec pre polomer elektrónu v danej hladine rne kde atóm má Z protónov je
podobne pre rýchlosť rne platí vzorec
Z týchto vzorcov si môžeme odvodiť vzorce pre energie, kde poznáme konštanty a hmotnosť elektrónu. Pre kinetickú energiu elektrónu je vzorec Eke
Pre elektrostatickú energiu elektrónu Eqe má vzorec záporné znamienko, pretože pôsobí proti kinetickej energii, vzorec je
Celková energia elektrónu vo vodíkovomo atóme má vzorec
Po dosadení dostaneme výsledný vzorec
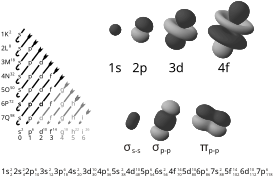
Môžeme si to predstaviť ako vlniaci mrak okolo jadra, pretože elektrón je zároveň častica ale aj vlnenie. Elektrón musíme uvažovať ako statickú vlnu okolo jadra. Elektróny obiehajú v orbitáloch. V každom orbitále môžu byť iba dva elektróny. orbitálov sú 4 druhy s p d f, ktoré sa líšia tvarom resp. koľko orbitálov môže byť v jednej vrstve. s orbitál môže byť iba jeden vo vrstve, p má 3 orbitály d 5 orbitálov f 7 orbitálov. Číslo pred orbitálom udáva v ktorej vrstve sa nachádza. v 7 vrstvách 1K 2L 3M 4N 5O 6P 7Q. počet orbitálov vo vrstvach 1K 1s, 2L 2s 2p, 3M 3s 3p 3d, 4N 4s 4p 4d 4f, 5O 5s 5p 5d 5f, 6P 6s 6p 6d, 7Q 7s 7p, ostatné orbitály nie sú obsadené. Dole na grafe vidno medzi ktorými orbitálmi môže preskočiť elektrón. Poradie je 1s; 2s; 2p->3s; 3d->4p->5s; 4f->5d->6p->7s; 5f->6d->7p. Elektrón preskakuje z nižšej vrstvy na vyššiu, do orbitálu ktorý má o 4 elektrony menej. Na grafe je zakreslené šípkami. Vedľa sú znázornené stojacie vlny orbitálov.
Dokopy môžu byť až 118 elektrónov tzn. že najťažší prvok má protónové číslo 118. Tento prvok bol už umelo vytvorený, nazvali ho Osmium.
Z rovnice momentu hybnosti si môžeme určiť hybnosť elektrónu pe a vlnovú dĺžku λe elektrónu podľa rovnice
Energiu môžeme prepočítať aj na energiu fotónu
z toho môžeme určiť aj zdanlivú hybnosť fotónu pf
Tieto vzorce môžeme použiť aj na iné častice. Častice môžeme urýchliť aj na rýchlosť blízku rýchlosti svetla, potom ale musíme zarátať aj relativistickú hmotnosť častice do vzorca, m=γm0. Úplný vzorec pre de Broglieho vlny je
λ je vlnová dĺžka častice m hmotnosť častice a v je rýchlosť častice. Znamená to, že častica je zároveň aj vlna, má svoju vlnovú dĺžku λ. Tieto vzorce boli mnoho krát dokázané. Prvý krát na princípe rozptýlenia, (difrakcii pomalých elektrónu pri dopade na kryštály niklu. Meranie vzdialenosti difrakčných čiar na tienidle potvrdilo správnosť výpočtov. Tým bolo potvrdené, že aj elektróny sa šíria aj ako vlny resp. že elektrón je vlna a zároveň častica. Bol to správny predpoklad, že všetky častice včítane molekúl sa môžu šíriť duálne. Dnes na tom princípe pracujú napr. elektrónové mikroskopy.
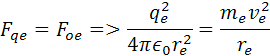
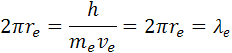
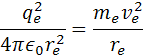
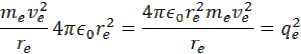
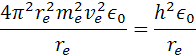
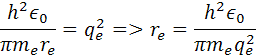
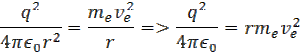
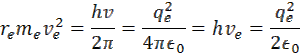
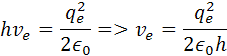
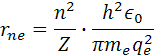
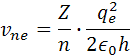
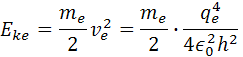
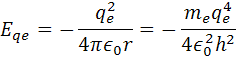
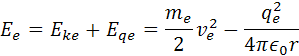
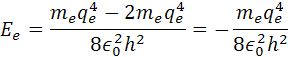
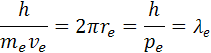
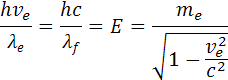
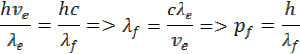
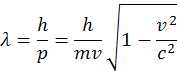




















dobry fyzik vie povedat myslienku bez pouzitia ...
veľmi pekne ďakujem za príspevok. momentálne ...
+++ ...
Zdravím. Pozrel som si blog,nemám veľmi čas ...
Celá debata | RSS tejto debaty