aldebaran.pravda.sme

Planck v podstate upravil Wienov vzorec a z neho presne vypočítal hodnotu konštanty h. Neviem prečo Rayleigh a Jeans urobili takú školácku chybu vo výpočtoch, keď mali skoro presný Wienov vzťah. Planckov vzťah popisuje presne celé spektrum žiarenia úplne čierného telesa v závislosti na frekvencii aj na vlnovej dĺžke. Doplním ešte minulé blogy o frekvenciu. Vzťah pre hustotu žiarenia v závislosti na frekvencii B(ν, T) podľa minulého blogu odvodime deriváciou dc/dλ. Keďže násobky sú číselne rovnaké derivujeme iba prvý člen podľa vzorca

Hustota žiarenia vyjadrenú frekvenciou je v podstate súčet energie rovnakých elektromagnetických vĺn, ktoré prechádzajú  cez steradián. Exponenciálne násobky sú číselne rovnaké, len sa zamení vlnová dĺžka za frekvenciu podľa vzorca

Z toho vychádza vzťah pre spektrálna hustota žiarenia vyjadrenú frekvenciou B(ν, T)

Grafy vyjadrené frekvenciou sú presnejšie, pretože začínajú od nuly. Dole je frekvenčný graf hustoty spektrálneho žiarenia  pri teplote 5800°K.  Modrá krivka zodpovedá Planckovmu vzťahu, červená je Wienov vzťah a čierna čiarkovaná čiara zodpovedá Rayleigh – Jeansovmu vzťahu. Na vodorovnej osi je daná frekvencia spektra, na zvislej osi je hustota žiarenia. Žiarenie vychádza z bodového zdroja a dopadá na steradián ktorý plochu 1m² ako výkon za impulz resp. KW/m²THz. Pri danej teplote T úplne čierneho telesa vieme určiť presne pre danú frekvenciuje ν. hustotu žiarenia B(ν, T).

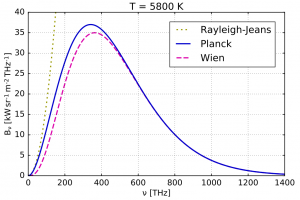
Na krivke pre vlnové dĺžke je vrchol na krivke  λ_max=b∙T , ale pri frekvencii vrchol krivky nezodpovedá ν_max=c/λ_max, pretože vziorec pre frekvenciu B(ν, T).má iné hodnoty ako vzorec vlnvej dĺžky B(λ, T). V minulom blogu som odvodil hodnotu x z derivácie funkcie B(λ, T) na vlnovej dĺžke λ. Hodnotu x pre frekvenciu dostaneme podobne, derivujeme funkciu B(ν, T) na frekvencii ν. Výsledný vzore po derivácii je

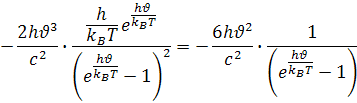
po vykrátení dostávame vzorec

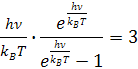
Podobne ako v odvodení podľa vlnovej dĺžky, vyrieši sa to pomocou Lambertovej W funkcie ktorá má vzorec

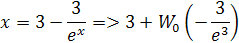
Z toho vychádza x = 2.821439372122078893. táto hodnota sa tiež označuje písmenom α. Maximálnu intenzitu frekvencie ale musíme počítať inak, pretože vrcholy v grafoch sú iné. Vzorec pre ν_max odvodíme z hodnoty λ_max podľa rovnice

Vložením hodnoty α pri danej teplote T získame vzorec pre frekvenciu ν_max

Wien predpokladal a dokázal, že existuje nejaká najmenšia prevodná konštanta medzi frekvenciou a energiou elektromagnetickej vlny pri frekvenciách, ktoré sa generujú teplom telies. Planck Porovnal Wienov vzťah s Rayleigh – Johnsonovím vzťahom a z toho usúdil, že v hmote pôsobením tepla sa rozkmitajú atómy ako oscilátory s rôznymi frekvenciami, podľa toho akú dostanú energiu, ktorú vyžiaria ako elektromagnetické vlny. Planckova konštanta je najmenšia konštanta, preto môžeme predpokladať, že menšia hodnota energia ako h nemôže byť. Keďže energia elektromagnetického žiarenia s vysokou frekvenciou je násobok frekvencie a Planckovej konštanty, môžeme sa domnievať, že energia svetelných vĺn sa šíri nespojite. Znamená to že frekvencie elektromagnetického žiarenia, ktoré sa generujú teplom, nemôžu byť zlomkové ale celočíselné. Malé frekvencie sa generujú zmenou zmenou elektrického a magnetického poľa v podstate anténou. Vlny s takou frekvenciou sa šíria spojite a ich energia je závislá na elektrickej a magnetickej intenzite.

V roku 1887 Nemecký fyzik Rudolf Hertz robil pokusy s elektromagnetickými vlnami. Na generovanie elektromagnetických vĺn používal iskrište, ktoré bolo kvôli detekcii uzavreté v tmavej komore. Pri pokusoch do komory s iskrišťom vkladal kovové pásiky, rôznych druhov kovu. Keď ich vyberal zistil, že majú kladný náboj. Rovnako veľké platničky ale z rôznych kovových materiálov mali nerovnako veľký náboj. Neskôr robil pokusy, kde osvetľoval plochy rôznych druhov kovov svetlom jednej vlnovej dĺžky pod určitým uhlom. Meraním zistil, že z kovu začali vyletovať elektróny, preto boli platničky kladné. Kinetická energia elektrónov nezávisela od intenzity svetla ale od frekvencie svetla a druhu kovu. Od intenzity závisel iba počet elektrónov. Tento jav nazval fotoelektrický jav. Matematicky ho vysvetlil Einstein a za tento objav dostal Nobelovu cenu. Einstein si uvedomil,  že ak je frekvencia svetla celočíselná, tak jeho energia sa bude šíriť v určitých balíkoch elektromagnetických vĺn. Celkový balík energie nazval fotón a jeho energia E_f je má taký istý vzorec ako vypočítal Planck do exponentu E_f=hν.  Počet vĺn v jednom balíku určuje frekvencia. Znamená to balíky energie v svetelných vlnách môžeme považovať za častice svetla, Einstein tieto častice svetla nazval fotóny. Pri vysvetlení fotoelektrického javu Einstein uvažoval, že keď energia fotónov závisí iba od frekvencie f podľa vzorca E=h∙f, tak na uvoľnenie elektrónov museli fotóny vytvoriť určitú prácu a zvyšok energie fotónov sa zmenil na kinetickú energiu elektrónov. Rôzne materiály ktoré emitujú elektróny, začínajú ich emitovať pri určitých najmenších frekvenciách f₀. Znamená to, že energia najmenšej frekvencie je U₀=h∙f₀. Potom  rozdiel energie fotónu a minimálnej energie pri ktorej uvoľní fotón elektrón je  kinetická energie elektrónov T. Podľa toho zostavil Einstein vzorec pre kinetickú energiu elektrónov.

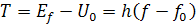
Z toho nám vyplýva, že aj kinetickú energiu elementárnych častíc hmoty môžeme vyjadriť frekvenciou. Znamená to, že aj energia elementárnych častíc sa nešíri spojite, ale v určitých balíčkoch energie. Tieto balíky energie nazval Einstein kvanta. Z toho vznikol názov kvantová fyzika. Einstein a Planck boli zakladatelia kvantovej mechaniky. Niekedy sa vo výpočtoch v kvantovej fyzike používa uhlová frekvencia ω=2πf. Vtedy sa požíva redukovaná Planckova konštanta  ħ. Vzorec pre hodnotu redukovanej konštanty je ħ=h/2π.

Cez výpočet výkonu energie svetelných spektrálnych vĺn sa prišlo na poslednú konštantu vesmíru, ktorá je najmenej známa ale dobre merateľná a v poslednom období dosť významná. Ostatné konštanty sa môžu odvodzovať podľa rýchlosti svetla a Planckovej konštanty, dokonca kilogram je definovaný prostredníctvom Planckovej konštanty. Je to preto, lebo Planckova konštanta je dnes najlepšie merateľná konštanta.