Reagujem na článok Stan.021 ktorý písal o zadaní výpočtu v Amazone pri vstupných pohovoroch. Zadanie bolo: vypočítať vzdialenosť stĺpcov keď bude 80m lano visieť na 50m stĺpcoch a najmenšia vzdialenosť lana od zemi je 20m. je to v rovine.
Stan.41 tam odvodil rovnicu pre reťazovku. Na reťazovku podľa grafu pôsobia 3 sily. Sila ktorá ťahá reťazovku k zemi je vlastne váha. Označená je λgs, Sila T0 pôsobí na reťazovku tak ako keby ju naťahovala a T je výsledná sila. Podľa grafu dole sú naznačené smery síl.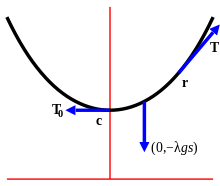 λ je hmotnosť na jednotku dĺžky g je gravitačné zrýchlenie s je polovičná dĺžka reťaze. Podľa grafu dole a je najmenšia výška. Hmotnosť polovice reťaze je λ·s. Pre konštrukcie nejakých stavieb napr. laná na mostoch sa musia navrhovať presne všetky rozmery, dĺžky lana, výšky stĺpcov, a vzdialenosti od zeme. Dole na grafe je ukázané ako vyzerajú reťazovky vzhľadom na ich rozmery.
λ je hmotnosť na jednotku dĺžky g je gravitačné zrýchlenie s je polovičná dĺžka reťaze. Podľa grafu dole a je najmenšia výška. Hmotnosť polovice reťaze je λ·s. Pre konštrukcie nejakých stavieb napr. laná na mostoch sa musia navrhovať presne všetky rozmery, dĺžky lana, výšky stĺpcov, a vzdialenosti od zeme. Dole na grafe je ukázané ako vyzerajú reťazovky vzhľadom na ich rozmery.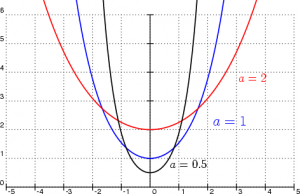
Na tomto grafe sú v rovnakej výške na osy y môže to odpovedať výške zavesenia lana. Označenie a udáva vzdialenosť od osy x. a je parameter reťazovky, opačne orientované udáva vzdialenosť ohniska reťazovky. Dĺžka reťaze na grafe je rovnaká. Mení sa vzdialenosť zavesenia reťazovky, je to znázornené na osy x.
Preto pri výpočte kde potrebujeme vypočítať reťaz tak aby splňovala tie podmienky musíme mať zadané iba dva parametre. Alebo keď sú zadané tri tak si môžeme overiť či ten jeden je správny pre reťazovku tak aby bola namáhaná optimálne. Najčastejšie sa udáva vzdialenosť stĺpa a najnižší bod lana, resp. reťaze. Nebudem teraz odvodzovať vzorec pre reťazovku ani hyperbolické funkcie, len napíšem ako vyzerajú vzorce pre reťazovku. Pre výšku stĺpca je vzorec
y je výška sĺpca x je polovičná veľkosť reťaze, a je parameter a cosh je hyperbolický kosínus. Keď je reťazovka v rovine súmerná tak je to vlastne najmenšia vzdialenosť od zeme. Keď nepoznáme x ale poznáme polovicu dĺžky lana s a parameter a môžeme vypočítať x podľa vzorca
argsinh argument hyperbolického je tzv. inverzná hodnota hyperbolického sínusu sinh. Keď x to vložíme do vzorca dostaneme vzorec
Ten výpočet je taký ako keby sme poznali dĺžku oblúka na kružnici, jeho výšku od osi x a mali vypočítať uhol aj polomer. My poznáme dĺžku hyperboly resp. reťazovky a to je komplikovanejší prípad ako kružnica. Zadané hodnoty sú a=20m, s=40m a y=50m. Z týchto hodnôt si môžeme urobiť skúšku správnosti. vložíme hodnoty do vzorca pre výpočet veľkosti stĺpca kde poznáme polovicu dĺžky lana. y nám musí vychádzať 50m Vo vzorci ale výsledok je iný preto potrebujeme iný vzorec.
Vo vzorci kde je výsledok iný potrebujeme odvodiť parameter a pomocou previsu lana d, pretože a+d=y
Pre túto reťazovku je vzorec po úprave
y je výška stĺpc a p je predlženie stĺpca. Vzorec pre predlženie je p=y-(d-a). d je previs našom prípade y-d je vzdialenosť od zeme 20m. Parameter a môžeme vypočítať len nejakou numerickou metódou na excely. Postupne budeme dosadzovať dosadzovať za a nejakú hodnotu až dostanem výsledok 50. Do jednej bunky som vložil vzorec
Za a sa bude dosadzovať nejaké číslo z inej bunky. Aby sme jemne priratávali tak bunku si upravíme tak, že nám bude deliť bunku kde budeme udávať hodnotu prvočíslom. Zadal som deliteľa 3. Keby sme začali 30 tak bunka vydelí 3 a 10 vpíše do vzorca. Postupne dáme 31/3, 32/3 a pri 35/3 by sme zistili, že bunka bude mať hodnotu 50.Tak sme vypočítali hodnotu a=35/3. Rozpísaní dostaneme vzorec pre x
dĺžka vzdialenosti stĺpcov je 2x z toho vychádza výsledná rovnica
Po dosadení hodnôt dostaneme výsledok vzdialenosti stĺpcov 2x=45,40457014 m
Ako sme sa k tomu vzorcu dostali napíšem nabudúce.
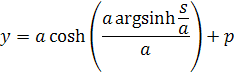
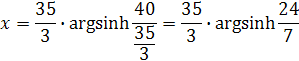



















nie pokiaľ máš pevne zavesené a pevné lano ...
aj od teploty. navrhy sa robia u nas pre teplotu ...
tvar priehybovej paraboly podla mna zavisi od ...
kalkulačkou sa to nedá pretože pochybujem, ...
a preco nie, skuste kalkulacku a vychadza to. ...
Celá debata | RSS tejto debaty