Ako som písal v minulom blogu preveriť Einsteinovu teóriu o relativistickej hmotnosti môžeme iba pri kinetickej energii. Energia je schopnosť konať prácu. Kinetickú energiu má teleso v pohybe. Keby sme dali do cesty letiaceho telesa nejakú prekážku tak pri náraze časť energie sa zmení na prácu. Mechanická práca sa dá zmerať rôznymi spôsobmi. Vzorec pre kinetickú energiu Ek je![]() Hmotnosť m je pred integrálom pretože sa nemení. Keďže je tam ½ tak môžeme vzorec takto rozpísať. Keby sme mali teleso pohybujúce sa rýchlosťou v blížiacou sa rýchlosti svetla c tak musíme do vzorci vložiť relativistickú hmotnosť. Do poslednej rovnice vložíme relativistickú hmotnosť podľa vzorca
Hmotnosť m je pred integrálom pretože sa nemení. Keďže je tam ½ tak môžeme vzorec takto rozpísať. Keby sme mali teleso pohybujúce sa rýchlosťou v blížiacou sa rýchlosti svetla c tak musíme do vzorci vložiť relativistickú hmotnosť. Do poslednej rovnice vložíme relativistickú hmotnosť podľa vzorca 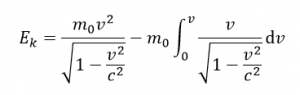
Pred integrálom je hmotnosť m0 pretože táto hmotnosť sa nemení.
Ten sa nedá jednoducho vypočítať ale môžeme si člen pod odmocninou nahradiť tzv. substitúciou t podľa vzorca
podľa toho si môžeme určiť derivovaním diferenciál dv podľa vzorcov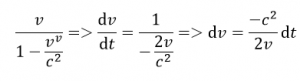
a vložíme za c2/2v do integrálov podľa vzorca 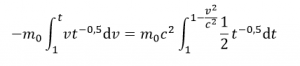
c2 ide pred integrál pretože je to konštanta. Pri integrovaní postupujeme tak, že k mocnine priratávame 1 a delíme výslednou mocninou. V našom prípade podľa vzorca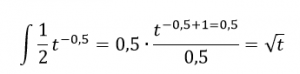
Určitý integrál integrujeme tak, že si vynásobíme členom pred integrálom výslednú mocninu a odčítame dolný index horného. Výsledná je odmocnina z t tak odmocninu násobíme m0c2 a odmocnina z 1 je 1 tak vynásobíme jednotkou m0c2 a odčítame podľa vzorcov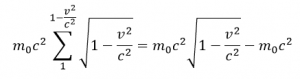
Potom vložíme do pôvodného vzorca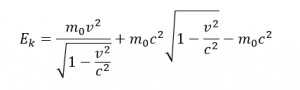
Roznásobením a vykrátením dostaneme konečný vzorec pre kinetickú energiu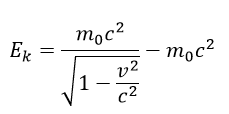
Einstein kinetickú energiu Ek prepísal na vzorec pre celkovú energiu E a kľudovú, nulovú energiu E0 podľa vzorca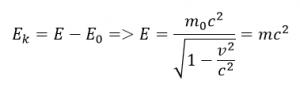
Celková energia E je jeho slávny vzorec ktorý je prepočet medzi hmotou a energiou![]()
Toto je vzťah medzi hmotou a energiou. Znamená to, že v hmote je ukrytá obrovská energia. Ale ako ju dostať z hmoty. Zaujímavé na tom je, že práve nacistický vedci začali overovať Einsteinovu teóriu. Čo keby sme zo zlomku hmoty vyrobili energiu, mohli by sme mať bombu ktorá zrovna veľkomesto. Nabudúce o tom niečo napíšem.
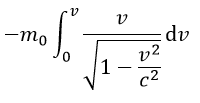
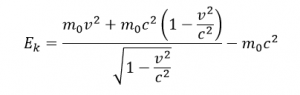
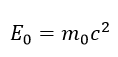




















Celá debata | RSS tejto debaty