V škole sme sa učili, že objem gule je 4/3∙πr3. Tento vzorec sa dá pomerne ľahko odvodiť pomocou integrálov, ale nie každý by tomu rozumel pretože funkcia na integrovanie je pomerne zložitá. Objem gule si môžeme sčasti nahradiť objemom naskladaných valčekov s rovnakou výškou ktoré sa dotýkajú jednou podstavou povrchu gule. Vyzerá to ako pyramída v gule. Čím bude tých valčekov viac tým výpočet objemu gule bude presnejší. Keď bude tých valčekov nekonečné množstvo, tak ich celkový objem sa bude rovnať objemu gule. Pre názornosť som nakresli taký nepodarený obrázok, ale na pochopenie to stačí. Rozdelíme guľu na polovicu. Polomer rozdelíme na rovnakých n časti, zmestí sa tam n-1 valčekov.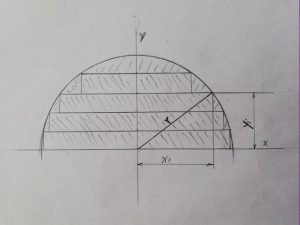
Na obrázku je znázornený rez vrchnej pologule v ktorej sú uložené valčeky, tak ako som opísal. Objem valčeka je podstava krát výška. Výška v našom prípade je výška válčeka v=r/n. Podstavu má každý valček inú, pretože každý má iný polomer. Jeho polomer označíme ako xi. je to preto lebo jeho polomer je rovnobežný s osou x a i určuje poradový valček od osy x. Ja som si rozdelil polguľu na 5 častí tzn. že sú tam 4 valčeky. Polomer r sa dotýka 3. valčeka na vrchnej podstave. Dostávame pravouhlý trojuholník, kde je vyznačené strany yi, xi a prepona r. hodnotu yi má vzorec yi=r∙i/n. Podľa Pytagorovej vety si môžeme odvodiť (xi)2 podľa vzorca
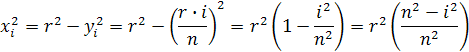
Objem valčeka má vzorec Vv=πr2∙v. Vložení do rovnice hodnoty pre xi a v dostaneme vzorec pre objem daného valčeka
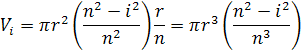
Celkový súčet válčekov je (n-1). V jednotlivých válčekoch sa mení vo vzorci i2 podľa vzoru 12+22+32+42…. Z toho dostávame vzorec pre súčet objemu válčekov VΣVi
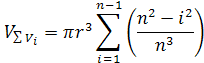
Keďže v sume sa mení iba i tak si môžeme vzorec pre sumu upraviť podľa vzoru
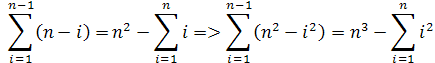
vydelenim n3 dostaneme vzorec
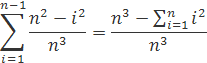
Z toho dostávame vzorec pre súčet objemu valčekov VΣVi
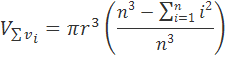
Čím bude n väčšie, tým presnejší výsledok dostaneme. Výpočet sumy kde n je vysoké je veľmi prácny. Musíme nájsť nejaký systém ako spočítať ľubovoľný počet prirodzených čísel, ktoré idú za sebou. Môžeme si to predstaviť na rovnováhe páky. Aby na páke nastala rovnováha musí byť súčet točivých momentov F∙r rovnaký na oboch poloviciach. Jeden príklad je znázornený je na spodnom obrázku.
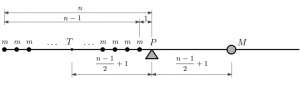
Na závažia pôsobí gravitačné zrýchlenie rovnako, preto budeme uvažovať iba hmotnosti m a vzdialenosť od bodu P. Vzdialenosť medzi bodom P a posledným závažím je n. Uvažujme, že vzdialenosť medzi dvoma závažiami aj medzi prvým závažím a bodom P je 1. Predpokladajme, že závažia sú rovnaké. Potom pre prvé platí m∙1, pre druhé m∙2 a postupne až pre n-té závažie m∙n. Chceme ho nahradiť jedným závažím o hmotnosti M na druhej strane, ktorého hmotnosť rovná sa súčtu závaží na druhej strane páky. Keďže závažia sú rovnaké tak ich násobíme ich počtom. Keďže vzdialenosti medzi závažiami je 1, tak počet závaží je n. Dostaneme vzorec M=m∙n. Aby páka bola v rovnováhe, tak vzdialenosť hmotnosti M od bodu P sa musí rovnať vzdialenosti ťažiska na druhej polovici páky. Ťažisko je medzi dvoma koncovými závažiami je presne v strede, pretože hmotnosti a vzdialenosti sú rovnako rozložené. ale ťažisko je v strede medzi závažiami. Keď bude vzdialenosť medzi závažiami 1 tak celková vzdialenosť medzi závažiami je n-1. Na páke sú závažia posunuté o 1. Podľa toho si môžeme určiť vzdialenosť ťažiska d, ktoré sa rovná vzdialenosti bodu P. Z toho môžeme odvodiť vzorec
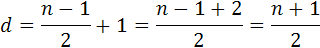
vynásobením hmotnosti m dostaneme vzorec
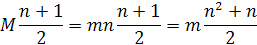
Keď vyhodíme m dostaneme vzorec pre sumu n kde i je prirodzené číslo od 1 až po n
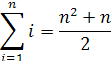
Ale mi máme súčet druhých mocnín. Tiež sa to dá znázorniť na rovnováhe na páke, ale hmotností je tam viac. Znázorňuje to obrázok dole
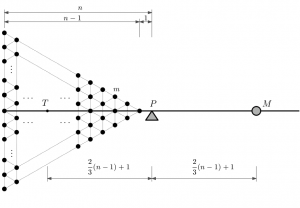
Závažia sú rozložené do radov, ktoré nasledujú za sebou tak, že každý rad má o jednu hmotnosť viac. Zavážia majú medzi sebou rovnakú vzdialenosť, preto vytvárajú rovnostranný trojuholník na osi, podľa obrázku hore. Výsledná hmotnosť M v tom prípade je súčet všetkých hmotností
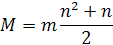
Pretože zavážia vytvárajú rovnostranný trojuholník mení sa vzdialenosť d. Rovnostranný trojuholník môžeme rozdeliť podľa obrázka dole na 6 pravouhlých trojuholníkov, ktoré majú uhly 30°, 60° a 90°. na obrázku vidno, že výška trojuholníka je zároveň aj jeho ťažnica. Ťažnica je zložená z kratšej odvesny a prepony pravouhlého trojuholníka. Keďže pravouhlý trojuholník má jeden uhol 30°, tak jeho sínus je 0,5 tzn. že prepona je 2 krát väčšia ako kratšia odvesna. Z toho vyplýva, že ťažisko rovnostranného trojuholníka je od vrcholu vzdialené 2/3 jeho výšky.
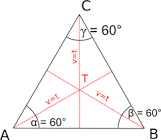
Z toho vychádza vzorec pre vzdialenosť ťažiska
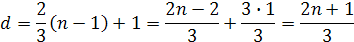
Vynásobením hmotnosťou m dostaneme rovnicu
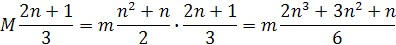
odobratím hmotnosti m dostaneme vzorec pre sumu druhých mocnín i2
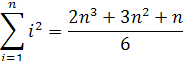
rozpísaním sumy v pôvodnom vzorci získame rovnicu
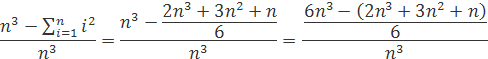
odčítaním 6n3–4n3 a vydelením čítateľa aj menovateľa n3 dostaneme vzorec
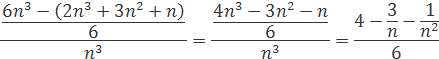
vložíme do vzorca a získame výsledok
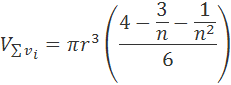
keď použijeme nekonečne veľa válčekov dostaneme výsledok pre pologuľu
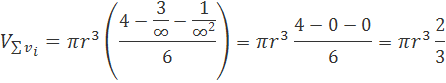
Kedže guľa má dve pologule vynásobením dvoma získame objem gule Vg
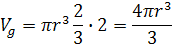




















Celá debata | RSS tejto debaty