aldebaran.pravda.sme

Trochu neskoro reagujem na článok o elipse, ktorý písal pán Bednár. V jeho blogu je uvedené, že veľkosť obvodu elipsy sa nedá vypočítať. Skutočne je to čiastočné pravda, skúsim to vysvetliť. Keď uvážime fakt, že π má nekonečne veľa číslic za desatinnou čiarkou tak ani veľkosť kružnice sa presne nedá vypočítať. Najprv vysvetlím niečo o elipse. Elipsa je v podstate roztiahnutá kružnica, kde polomer kružnice sa rozdelí na dve ohniská. Parametre elipsy sú popísaná na spodnom obrázku

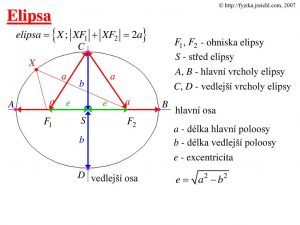
Charakteristická vlastnosť elipsy je excentrita e. Podľa obrázka vidno, že je to vzdialenosť ohniska od stredu elipsy. Vzorec je

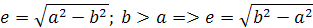
Elipsu môžeme považovať za sploštenú kružnicu. Pri kružnici a=b je excentrita nulová. Najväčšie sploštenie je vtedy keď a alebo b je nula. Znamená to, že keď jedna poloos sa bude blížiť k nule dĺžka obvodu elipsy sa bude blížiť k štvornásobku väčšej poloosi. strana prelínajú. Na výpočet obvodu sa používa približný výpočet, ktorý ale pri jednej veľmi malej poloosi je veľmi nepresný. Vzorec je

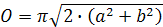
Presnejší výpočet dostaneme integráciou diferenciálu uhlu dt, pretože elipsa sa dá opísať aj oblúkovými mierami. Diferenciálu dt som odvodil v blogu Načo sú nám integrály. Vzorec pre diferenciál je

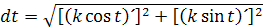
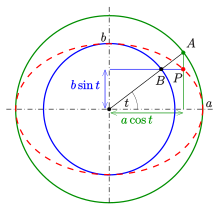
Z horného obrázku môžeme určiť vzdialenosti x a y podľa uhlu t

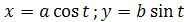
ich derivácie majú vzorce

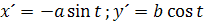
z toho vychádza diferenciál

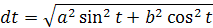
Z toho pre prvý kvadrant dĺžky elipsy môžeme odvodiť integrál

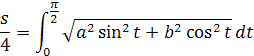
upravením podľa vzorcov, vyjadríme cosínus ako sinus

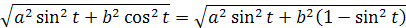
roznásobíme

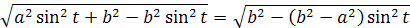
vyberieme pred odmocninu b

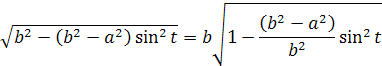
Takto získame výsledný integrál pre dĺžku prvého s/4 kvadrantu elipsy kde b>a

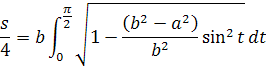
Z toho integrál pre výslednú dĺžku s kde je b>a má vzorec

pre a>b platí integrál

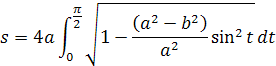
Násobky sínusov môžeme považovať za konštanty podťa vzorcov

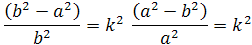
integrály si môžeme prepísať podľa konštanty do vzorcov

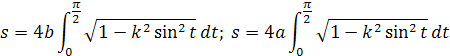
Tieto integrály sa nedajú jednoducho integrovať, pretože sínus sa mení konštantou z toho dôvodu sa nedá nahradiť substitúciou. Je to tzv. eliptický integrál E(k; φ) , ktorý má vzorec

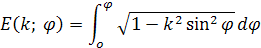
Ale pretože poznáme mieru sploštenia, číselnú excentritu e tak môžeme navrhnúť nejaký algoritmus kde postupným zmenšovaním obvodu kružnice s polomerom a sa budeme približovať k obvodu elipsy O.  Integrál sa počíta podľa nekonečného rádu zo vzorca

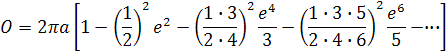
Pre b>a bude sa počítať excentrita opačne preto miesto 2πa bude 2πb. hodnoty v hranatej zátvorke sa pohybujú od 1 až do 2/π. 1 je keď e=0 tzn. že je to kružnica. Keď e sa rovná jednej poloosy tak kružnica je tak stlačená že je priamka. Vtedy je elipsy priamka, ktorá má iba dve poloosi na osi x resp. y. Ale keďže elipsa má 4 kvadranty tak celková dĺžka elipsy bude 4a resp. 4b. Od týchto krajných hodnôt sa odvodil tento Taylorov rad. Čím presnejší výpočet potrebujeme tým ten rad musí byť väčší. V praxi nepotrebujeme počítať veľmi presne napr. na výpočet kružnice stačí 3,14.

Budem rád keď si to niekto aj prečíta