aldebaran.pravda.sme

Pokračujem v mojich apolitických blogoch. Bol som prekvapený, že na takú nezaujímavú a otravnú tému, matematika bola aj diskusia.

Napier zistil pri určovaní čo najlepšieho základu prišiel na to, že pri určitom základe je krivka logaritmov plynulá. Napier zrejme netušil na aké dôležité číslo prišiel,až Euler o 100 rokov neskôr určil vzorec na výpočet základu prirodzených logaritmov. Vrátim sa ešte k Napierovi. V dobe Napiera sa rozvíjala astronómia, (Kepler. Bola potreba zložité čísla násobiť a deliť. Keďže násobenie čísla a delenie pri rovnakom základe mocnín sa robí obyčajným sčítaním, napadlo Napiera urobiť obrátenú funkciu k funkcii y=a^x kde by som poznal y a základ a si určil každému číslu mocninu kde základ a by bol zvolený podľa dohodnutého čísla. Znamená to, že ku každému číslu sa dá priradiť mocnina keď máme rovnaký základ. Potom môžeme jednoducho exponenty sčítať alebo odčítať podľa toho či budeme násobiť alebo deliť. A podľa výsledného exponentu si ho nájdeme v nejakých tabuľkách. Nazval exponenty logaritmus zo slov logos ritmus, opakovanie čísla podľa určitého postupu. Najprv zvolili za základ číslo 10 pretože to bolo najlepšie pochopiteľné. Jeho celistvé násobky sa jednoducho sčítali a pripisovala sa iba 0. Napr. zvolím si základ 10 mocnina bude 1. Keby som násobil 10_*10=100, mohol by som to podľa mocnín napísať 10¹⁺¹=10². Takto môžeme každému číslu dať nejaký exponent pri rovnakom základe. Majme napr. exponent pri 0,5 pri základe 10. Je to druhá odmocnina z 10 čo je približne 3,162278.. Pokiaľ budeme mať mocninu 1,5 tak si vynásobíme 10¹_*10^0,5 bude to 31,62278. Keď si vydelíme 10/100 dostaneme 0,1. Keby sme si to chceli napísať cez mocniny so základom 10 dostávame 10¹/10²=10^2-110^-1=0,1. Toto je princíp logaritmického počtu kde sme zvolili základ 10. Jeho zápis je log10=1.

Urobili si dostatočne presný graf po určitý logaritmus. Na xovú os nanášali čísla a na ypsilonovej osy odčítavali logaritmy. Ten graf si postupne zväčšovali a tak mohli v pohode čísla odčítavať.. Podľa toho logaritmus pri základe 10 sú čísla log10=1, log1=0. Nultá mocnina je vždy 1 preto log 1=0. Odmocnina z 10 je aj hocijaké číslo od 1do 10. Napr. 9 je 10^0,954243. Potom log9=0,954243 . Ako som písal odmocnina je vlastne mocnina kde exponent je menší ako 1. To číslo 0,954243 je dekadický logaritmus čísla 9. Logaritmus so záporným číslom je číslo menšie ako 1. Pokiaľ máme desatinnú čiarku za celým desatinným číslom tak je to násobok odmocniny a exponentu s celým číslom, napr. 90=10_*9 =10¹_*10^0,954243=10^1+0,954243=10^1,954243. Sčítali sme logaritmy,

resp. exponenty 1+0,954243=1,954243 odčítame s tabuliek a máme výsledok násobenia. Graf funkcie y=logx je zrkadlový obraz funkcie y=a^x. Dole je obrázok pre graf prirodzeného logaritmu porovnaného s exponenciálnou krivkou e^x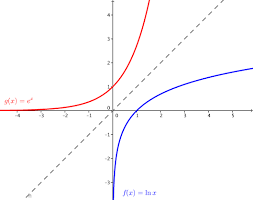

Dole je porovnanie logaritmických kriviek z rôzny základom. Červená krivka má základ 2, zelená ma základ e a modrá ma základ 10. Vidíme, že zelená krivka je najplynulejšia. Najmenej presná je krivka modrá zo základom 10. Napier pri určovaní čo najlepšieho základu prišiel na to, že pri určitom základe sa budú logaritmy dosť presne určovať, pretože ich krivka je najplynulejšia.  Bolo to to číslo čo neskôr nazval Euler Napierova konštanta e dnes je známe ako Eulerove číslo.

Napier ani nevedel ako to dobre urobil. Aj Newton vedel o tom čísle. Pravdepodobne tiež používal prirodzený logaritmus. Napier to číslo odvodil iba postupne ako ja na tých tabuľkách, neboli známe matematické postupy ktoré vytvoril Newton. Po 100 rokoch švajčiarsky matematik Leonhard Euler odvodil jeho vzorec. Použil metódu kde postupne zvyšoval základ čísla 2. Pochopiť sa to dá ke´d by niekto chcel veľmi zbohatnúť na úrokoch v banke. Urobil skúšobný vzorec s jednou neviem akú menu používal nazvem švédskou korunou na maximálny 100% úrok. Vložím jednu korunu do banky na jeden rok na 100%. Na konci roka dostanem korunu plus vložený úrok. Budem mať 2 koruny. Ale čo keby sme vložili korunu na pol roka a hneď by sme ju vložili na druhý polrok koľko dostanem peňazí. Za polrok dostanem 1+0,5=1,5 korún. 1,5 koruny vložím na druhý polrok na 50% úrok. Dostanem 1,5+0,75=2,25. Za rok budem mať z jednej korune pri 50% úroku na pol roka už 2,25 korún. Skúsim to urobiť tak že si úrok rozdelím na kvartál na 25%. môžem to rovno zapísať do vzorca, keď pre rozdelenie napíšem n

Keď to sčítam tak dostanem 1+0,25=1,25 za prvý kvartál, úrok som mal 0,25. Za druhý vkladám 1,25 a úrok budem mať 0,3125 výsledná suma bude 1,5625. Znovu vložím 1,5625 úrok bude 0,390625 výsledná suma za tretí kvartál je 1,953125. A nakoniec vo štvrtom kvartáli vkladám 1,953125 úrok mám 0,488281 a výsledná suma za 1 rok bude 2,441406 korún. Zase to presne výjde vo vzorci

Pre zaujímavosť, koľko by som teoreticky dostal v banke ktorá má 100% ročný úrok na vklady keď budem vkladať každý deň. Keď to vložím do vzorca dostanem sumu

Táto suma sa približuje k Napierovej konštante. Môžem si napísať vzorec tzv. limitu, Vo vzorci je označené k čomu sa bude určitý člen približovať. V našom prípade budeme exponent n sa bude blížiť k nekonečnu, ale nemôže byť nekonečno pretože by sme dostali 1, 1/nekonečno je nula a 1 na nekonečno je 1. Dostaneme vzorec

Tento vzorec ale môžeme vypočítať najpresnejšie tzv Taylorovým radom podľa vzoru

Takto by sme počítali až do nekonečna. Na konci by sme dostali 1/∞=0. Nechcem to správne opisovať iba som napísal princíp Taylorovho radu

Na čo je nám vlastne číslo e napíšem nabudúce.