aldebaran.pravda.sme

Ďalším dôležitým prvkom pre gravitáciu je gravitačné zrýchlenie.  Gravitačné zrýchlenie závisí už na hmotnosti. Gravitačné zrýchlenie zeme g zmeral Newton. Newton potvrdil, že telesa rôznej hmotnosti vo vákuu padajú z rovnakým zrýchlením. Keď pustíme dve telesá s nerovnakou hmotnosťou naraz z rovnakej výšky vo vákuu tak dopadnú v rovnakom čase. Výšku h z ktorej telesa padali poznáme a čas t sa dá zmerať. Pomer dráhy a času pri rovnomernom zrýchlení udáva priemernú rýchlosť. Priemerná rýchlosť je polovica najvyššej rýchlosti. S toho si môžeme odvodiť vzorec pre gravtačné zrýchlenie g

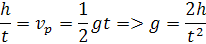
Gravitačné zrýchlenie na zeme g_z sa dá odvodiť z hmotnosti Zeme M_z, polomeru Zeme R_z. Gravitačné zrýchlenie klesá s výškou h. Z toho si môžeme odvodiť vzorec

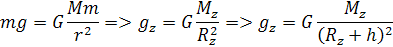
Ale okrem gravitačného zrýchlenia pôsobia ešte odstredivé sily na ktoré vplýva rotácia zeme. Tieto sily majú opačný charakter, znižujú gravitačné zrýchlenie. Výsledná sila ktorá pôsobí na povrchu Zeme je tiažová sila, je dobre znázornená na diagrame.

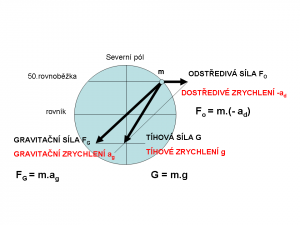
Vložením  hodnôt ktoré dnes máme dosť presne zmerané dostaneme hodnotu pre gravitačné zrýchlenie Zeme 9,8199 m/s ale vzhľadom na sploštenosť Zeme gravitačné hodnoty sú veľmi rozdielne, kolíšu okolo tejto hodnoty. Tiažovej sile zodpovedá tiažové zrýchlenie. Tiažové a gravitačné zrýchlenie má na rôznych miestach na zemeguli rôznu hodnotu. Na 45 stupni zemepisnej šírky g = 9,80665 m/s², na póloch g = 9,832 m/s² a na rovníku g = 9,780 m/s². Ako stabilné sa udáva tiažové zrýchlenie na 45 stupni zemepisnej šírky. Podľa tejto hodnoty môžeme kalibrovať aj silomer. zavesením 1 kg na pružinu nám vytvorí silu 9,80665 N Newtonov. Takú silu nazývame kilopond 1 kp=9,80665 N. Kilopond nie je v normalizovaných jednotkách, ale niekedy je veľmi praktický. Obyčajné váhy sú prakticky tiež silomery, ale budú pracovať pri rôznom gravitačnom zrýchlení rôzne, ale kilogram je stále kilogram v rôznych gravitáciách. 

Gravitačné zrýchlenie s dá dobre zmerať ale zmeranie gravitačnej konštanty Newton nemal čím, ale skúsil vypočítať zo známych hodnôt, Hmotnosť Zeme vypočítal ako hmotnosť guľe. Mernú hmotnosť Zeme určil podľa meraní hmotnosti určitých zemín. Hodnoty vložil do vzorca

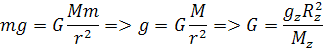
Podľa tejto rovnice Newton približne odhadol Gravitačnú konštantu G. Polomer zeme vypočítal podľa zakrivenia Zeme. Prepočítal polomer Zeme tak, že rozdelil poludníky na 360°. Medzi dvoma poludníkmi vyšla mu vzdialenosť na rovníku rovníku, 60 míľ, asi 97 km. Mernú hmotnosť odhadol na 5,5 násobok hmotnosti vody. Pri meraní gravitačného zrýchlenia g je presnosť závislá na presnosti merania času pádu telesasa t.  Dnes je hodnota gravitačnej konštanty G=6,67408×10^-11 m³/kgs². Zaujímavé je, že v prepočte na dnešné jednotky sa Newton len málo zmýlil pri tých hodnotách aké vypočítal z dovtedajších meraní.

Po Newtonovej smrti Anglický fyzik Henry Cavendish odmeral gravitačnú konštantu na torzných váhach. Gravitačnú konštantu G určil zo vzorca

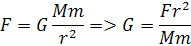
Torzné váhy pozostávali z dvoch ťažkých gúľ, ktoré stáli. Medzi nimi bolo zavesené rameno s dvoma malými guľami. Rameno bolo zavesené na striebornej niti presne v strede. zavesené rameno, ktoré malo malé guľové závažia činka s malými závažiami. Gravitačná sila pritiahla menšie gule na k veľkým, ktoré neboli pohyblivé. Podľa natočenia ramena, vedel akú gravitačnú silu vytvorili hmotnosti gúľ. Torzne váhy museli byť presne vypočítané, pretože gravitačné sily sú veľmi slabé. Hodnotu G vypočítal len s malou chybou, pretože mechanický systém nemôže byť veľmi presný.

Vrátim sa ku vzorcu pre hmotnosť okolo ktorého obiehajú planéty. Predstavme si Slnko okolo ktorého obieha Zem. Obieha po eliptickej dráhe. Poloos tejto dohody je súčet najmenšej a najväčšej vzdialenosti od Slnka. Stred Slnka leží na tejto úsečke ale nie v strede. Vydelenim dvomi dostávame vzdialenosť a. Táto vzdialenosť sa nazýva astronomická jednotka. V podstate je to stredná vzdialenosť Zeme od Slnka. Označuje sa AU. Keď zanedbáme hmotnosť Zeme tak môžeme vyrátať hmotnosť Slnka podľa vzťahu

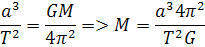
Čas obehu zeme T= 1 rok . Vo vzorci som to rozpísal na sekundy

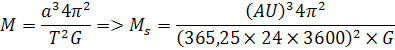
Hodnota AU = 1495987070 m, a hodnota G=6,67408×10^-11 m³/kgs².Keď tieto hodnoty vložíme do vzorca dostaneme hmotnosť Slnka M_S =1,9891×10³⁰ kg.