aldebaran.pravda.sme

Chcel by som vysvetliť odkiaľ sme zobrali vzorce pre reťazovku. Na to, že reťazovka nie je parabola ani hyperbola prišli to už dávno. Koncom 17. storočia reťazovku vysvetlil švajčiarský matematik Johann Bernoulli na základe gravitačných účinkov na reťaze. Použil som výrazy ktoré popisujú hyperbolický uhol, hyperbolický kosínus cosh, hyperbolický sínus sinh. V blogu je požitý aj inverzný hyperbolický sínus tzv. argument hyperbolického sínusu argsinh je označovaná aj ako sinh^-1. V budúcom blogu odvodím reťazovku, teraz pôjdem trochu odzadu. Derivácia reťazovky má vzorec

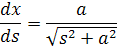
Aby sme vypočítali x musíme túto deriváciu integrovať. Ale nedá sa tento integrál priamo vypočítať. Reťazovka sa podobá na hyperbolu ktorá je dole na obrázku,

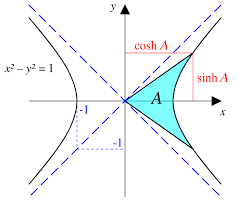
Môžeme si pomôcť z rovnice hyperboly. Keď vzdialenosť začiatku hyperboly na osi x od priesečníka os má hodnotu 1 platí rovnica

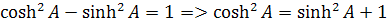
Môžeme upraviť túto rovnicu tak, že zameníme uhol A za funkciu u. dostávame rovnicu

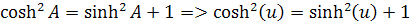
vynásobením tejto rovnice a² dostávame rovnicu

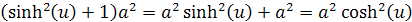
to môžeme vložiť do prvého vzťahu a dostávame upravený vzorec

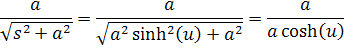
Podľa vzťahu medzi sínusom a inverným sínusom medzi uhlami 0°až 90°

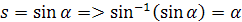
si môžeme odvodiť funkciu u

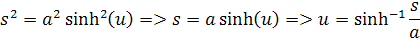
Aby sme vypočítali integrál musíme si odvodiť diferenciál ds podľa derivácie

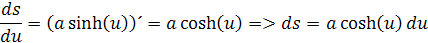
deriváciu sinh som odvodil dole

Vložením hodnôt do integrálu dostávame výsledný integrál

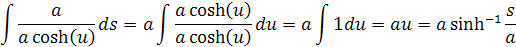
Z toho dostávame vzorec pre x

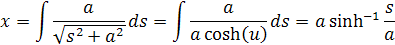
Funkcie sinh a cosh sú odvodené podľa vzorcov

Tieto funkcie odvodím v budúcich blogoch

derivácia funkcie e^x = e^x. Integrál derivácie je pôvodná z toho vychádza e^x = e^x. Môžeme to rozpísať do vzorcov

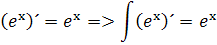
Derivácia v praxi znamená tangens uhla dotyčnice. Dotyčnica funkcie e^-x je na osi -x tzn. že derivácia musí byť záporná a z toho si môžeme odvodiť integrál

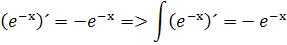
sinh integrujeme podľa vzorca

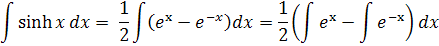
vložením hodnôt do integrálov získame cosh podľa vzorca

Podľa derivácii exponentov môžeme odvodiť aj deriváciu funkcie sinh

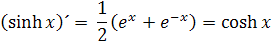
odtiaľ vychádza, že derivácia aj integrál sinh je cosh

Pre výšku stĺpca y vychádzame z derivácie

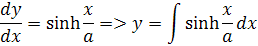
Pretože nemáme obyčajné x ale x/a musíme použiť transformáciu integrálu, podľa vzorca kde použijeme funkciu u

Vložíme do upraveného integrálu

Vložením za udu dostaneme výsledok pre výšku stĺpca y

V budúcom blogu napíšem celé odvodenie reťazovky. Reťazovka sa odvodzuje zo síl, ktoré na ňu pôsobia. Je to váha reťazovky a sila ktorá pôsobí na stred reťazovky vo vodorovnom smere. Sily sa odvodzujú z gravitačného zrýchlenia g a hmotnosti elementu reťazovky λ.