Heisenbergova teória neurčitosti potrebuje trochu predstavivosti. V minulom blogu som písal o pohybe elektrónov v otómovom orbitále. Opísal som ako matematicky vysvetlil de Broglie elektrónový orbitál ako vlnu. Heisenberg popisoval vonkajšie pôsobenie na elektrón. Vychádzal z fotoelektrického javu. Keď fotón vyrazí elektrón z hmoty, tak musí pôsobiť aj na pohybujúci elektrón. Keď fotón narazí do letiaceho elektrónu, zmení jeho polohu a tým pádom aj jeho hybnosť. Uvažoval, že medzi zmenou polohy a zmenou hybnosti elektrónu, musí byť určitá matematická závislosť. Keďže elektrón je vlna aj častica, vysvetlil svoju teóriu pomocou zákonov z optiky. Predstavil si mikroskop pod ktorým letí elektrón. dole je obrázok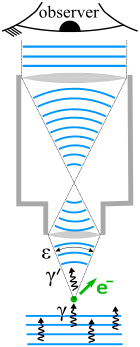 V momente keď bude elektrón e– pod mikroskopom tak ožiaria ho vysokoenergetické fotóny. Fotóny zmenia hybnosť elektrónu a vychýlia ho z dráhy. Pretože elektrón je aj vlnenie, tak fotóny budú interferovať, rozptýlia sa do uhla ε, ako pri rozptylovej šošovke. Hybnosť elektrónu sa zmení na určitom zlomku dráhy Δx. Čím bude fotón energetickejší, tým pádom bude uhol ε väčší tzn. dá sa lepšie zmerať zmena polohy elektrónu Δx. Môžeme zmerať interferovanú vlnu λ a uhol ε. Z toho môžeme odvodiť zmenu dráhy Δx
V momente keď bude elektrón e– pod mikroskopom tak ožiaria ho vysokoenergetické fotóny. Fotóny zmenia hybnosť elektrónu a vychýlia ho z dráhy. Pretože elektrón je aj vlnenie, tak fotóny budú interferovať, rozptýlia sa do uhla ε, ako pri rozptylovej šošovke. Hybnosť elektrónu sa zmení na určitom zlomku dráhy Δx. Čím bude fotón energetickejší, tým pádom bude uhol ε väčší tzn. dá sa lepšie zmerať zmena polohy elektrónu Δx. Môžeme zmerať interferovanú vlnu λ a uhol ε. Z toho môžeme odvodiť zmenu dráhy Δx
Zmenu polohy elektrónu môžeme považovať za odchýlku merania tzn. že polohu častice nemôžeme zmerať presne. Keďže poznáme zmenu polohy tak môžeme určiť aj zmenu hybnosti.
Z týchto nerovníc môžeme odvodiť vzťahy medzi Δx a Δp
Tieto nerovnice hovoria že nikdy nemôžeme presne zmerať polohu elektrónu pretože pri meraní sa mení ich hybnosť. Je to vysvetlenie dvojštrbinového efektu. Keď púšťali elektróny cez malé štrbiny tak vznikli na tienidle interferenčné obrazce. Vysvetlenie je, že pred štrbinou boli elektróny ale za štrbinou boli už fotóny. Je to dôsledkom toho, že keď prelietavali úzkou štrbinou, museli meniť svoju hybnosť. Táto teória vysvetľuje, prečo nemôžeme presne zmerať polohu elektrónu, pretože vždy je tam určitá odchýlka merania. Čím presnejšie chcem zmerať tým bude odchýlka väčšia. Je to geniálny úsudok, Heisenberg spojil časticu a vlnu do jednej rovnice.
Túto rovnicu spresnil americký fyzik Earle Hesse Kennard. Elektrón pri náraze fotónu zmení aj energiu za určitú zmenu času. Z Heisenbergovej rovnice sa odchýlka energie na odchýlke času nedá odvodiť. To viedlo Kennarda k oprave Heisenbergovho vzorca. Zobral pre odvodenie zmenu kinetickej energie elektrónu, ktorá nastane pri náraze fotónu. Polohu pohybujúceho telesa vieme pomerne presne zmerať. Aby sme zmerali rýchlosť pohybujúceho telesa musíme poznať jeho dve polohy na dráhe. Z nameraných hodnôt zmeny dráhy Δx a zmeny času Δt môžeme pomerne presne vypočítať priemernú rýchlosť vp. Pokiaľ poznáme hmotnosť môžeme určiť priemernú hybnosť pp a priemernú kinetickú energiu Ekp Pri časticiach sa nedá poloha tak zmerať, pretože ich kinetická energia je o veľa rádov menšia ako kinetická energia telies a častice sú zároveň aj vlny.
Zmenu polohy častice Δx si môžeme rozpísať podľa vzorca
Pri náraze elektrónu nastáva zmena energie elektrónu. Vieme zmerať jeho interferovanú vlnu a určiť jej energiu Eω . Zmenu energie si môžeme určiť podľa zmeny polohy Δx. Môže vychádzať z obehovej rýchlosti vo elektrónu ktorý má polomer r a dobu obehu T. Z toho nám vyšla uhlová rýchlosť ω. Podľa toho môžeme určiť aj energiu vlnenia Eω. Konštantu h musíme upraviť na redukovanú Planckovu konštantu ħ. Energiu vlnenia Eω
Energie elektrónu vodíka si môžeme určiť podľa uhlovej rýchlosti ω a polomeru r. Keď budeme kinetickú energiu uvažovať ako polovicu celkove energie, tak celkovú energia je hmotnosť krát rýchlosť na druhú. Podľa obehovej rýchlosti vo môžeme odvodiť úmeru medzi celkovou energiou E a energiou vlnenia elektrónu Eω .
Zmenu celkovej energie ΔE môžeme uvažovať ako kinetickú energiu z polomerom otáčania Δx, ale uhlová rýchlosť sa nemení. Preto zmenu energie vlnenia ΔEω musíme uvažovať ako polovicu Eω. Z toho môžeme odvodiť vzorec
pre hybnosť elektrónu vyjadrenú uhlovou rýchlosťou dostaneme vzorec
pre zmenu hybnosti dostaneme vzorec
Vynásobením rovnice hmotnosťou elektrónu me získame vzorec
z toho vzorca sme odvodili zmenu hybnosti na druhú
odmocnením dostaneme zmenu hybnosti Δp
Pre zmenu polohy Δx si odvodíme rovnicu zo zmeny hybnosti Δp podľa vzorca
vložíme do vzorca pre hybnosť a vykrátení dostaneme vzorec pre x2
odmocnením dostaneme vzťah pre zmenu polohy Δx
Opravený Heisenbergov vzťah má tvar
Ale pri predstave ako vyzerá neurčitosť polohy častice, už začína Schrödingerova teória. Je to veľmi dobre znázornené na spodnom obrázku.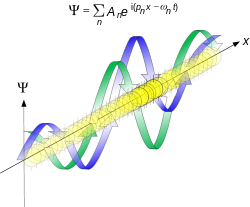
Časticu si musíme predstaviť ako vlnu, ktorá sa skladá z dvoch vĺn. Je to tzv. komplexná vlna. Má dve vlny, skutočná vlna, modrá a imaginárna vlna, zelená, ktoré sa pohybujú spoločne na osi x. Častica by sa mala presne nachádzať na skutočnej vlne. Imaginárna vlna sa vzďaľuje od skutočnej o neurčitosť Δx. Neurčitosť polohy je označená žltou farbou.Na obrázku je vidieť že amplitúda nie je rovnaká ako pri rovinnej vlne.
Odvodenie výpočtov je dosť komplikované, ale v anglickej wikipedii som našiel jednoduché odvodenie, ktoré pri troche predstavivosti postačuje. Je to trochu náročnejšie na predstavu, ale pri trochu predstavivosti je možné to pochopiť.
Budem rád keď si to niekto aj prečíta.
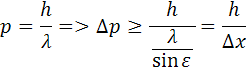
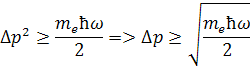
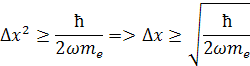
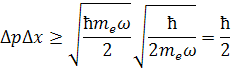




















ďakujem za reakciu. mám veľa wordov napísaných.... ...
uhol epsilon nemôže byť väčší ako 90°preto... ...
treba skusit napisat taku popularnu knizocku ...
Prepáčte, ale nerozumiem formulácii : " ...
dakujem za príspevok. vysvetliť niečo z kvantovej... ...
Celá debata | RSS tejto debaty